TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Orbitais atómicas.

Orbital atômico ^{(português brasileiro)} ou orbital atómica ^{(português europeu)} de um átomo é a denominação dos estados estacionários da função de onda de um elétron (funções próprias do hamiltoniano (H) na equação de Schrödinger ${\displaystyle H\psi =E\psi }$,

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 em que ${\displaystyle \psi }$ é a função de onda).^[1] Entretanto, os orbitais não representam a posição exata do elétron no espaço, que não pode ser determinada devido à sua natureza ondulatória; apenas delimitam uma região do espaço na qual a probabilidade de encontrar o elétron é mais alta.^[2]

• 6Referências

Números quânticos

• O valor do número quântico ${\displaystyle n}$ (número quântico principal ou primário, que apresenta os valores ${\displaystyle 1,~2,~3,~4,~5,~6~ou~7}$ [também representado por ${\displaystyle K,~L,~M,~N,~O,~P~e~Q}$
• 
  
• 
  
• ]) define o tamanho do orbital. Quanto maior o número, maior o volume do orbital. Também é o número quântico que tem a maior influência na energia do orbital.
• O valor do número quântico ${\displaystyle l}$ (número quântico secundário ou azimutal, que apresenta os valores ${\displaystyle 0,~1,~2,~...,~n-1}$) indica a forma do orbital e o seu momento angular. O momento angular é determinado pela equação:

${\displaystyle |L|=\hbar \cdot {\sqrt {l(l+1)}}}$

A notação científica (procedente da espectroscopia) é a seguinte:

• ${\displaystyle l=0}$, orbitais ${\displaystyle s}$
• ${\displaystyle l=1}$, orbitais ${\displaystyle p}$
• ${\displaystyle l=2}$, orbitais ${\displaystyle d}$
• ${\displaystyle l=3}$, orbitais ${\displaystyle f}$

• TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Para os demais orbitais segue-se a ordem alfabética.

• O valor do ${\displaystyle ml}$ (número quântico terciário ou magnético, que pode assumir os valores ${\displaystyle -l~...~0~...~+l}$) define a orientação espacial do orbital diante de um campo magnético externo. Para a projeção do momento angular diante de um campo externo, verifica-se através da equação:

${\displaystyle L_{z}=\hbar \cdot m}$

///////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

• O valor de ${\displaystyle ms}$ (número quântico magnético de spin ou spin) pode ser ${\displaystyle +1/2~ou~-1/2}$. O valor de ${\displaystyle s}$ que equivale a uma valor fixo ${\displaystyle 1/2}$.

Pode-se decompor a função de onda empregando-se o sistema de coordenadas esféricas da seguinte forma:

${\displaystyle \psi _{n,~l,~ml}=R_{n,~l}(r)~\Theta _{l,~m_{l}}~(\theta )~\Phi _{m_{l}}(\varphi )}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde

• ${\displaystyle R_{n,~l}~(~r)}$ representa a distância do elétron até o núcleo, e
• ${\displaystyle \Theta _{l,~m_{l}}~(\theta )~\Phi _{m_{l}}(\varphi )}$ a geometria do orbital.

Para a representação do orbital emprega-se a função quadrada, ${\displaystyle \left|\Theta _{l,~m_{l}}~(\theta )\right|^{2}}$ ${\displaystyle \left|~\Phi _{m_{l}}(\varphi )\right|^{2}}$ ,

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 já que esta é proporcional à densidade de carga e, portanto, a densidade de probabilidade, isto é, o volume que encerra a maior parte da probabilidade de encontrar o elétron ou, se preferir, o volume ou a região do espaço na qual o elétron passa a maior parte do tempo.

O modelo spherium consiste de dois elétrons presos na superfície de uma esfera de raio ${\displaystyle R}$. Ele tem sido usado por Berry e colaboradores ^[1] para entender tantos sistemas fracamente e fortemente correlacionados e sugeri uma versão "alternativa" para a regra de Hund. Seidl estuda esse sistema no contexto da teoria do funcional da densidade (DFT) para desenvolver a nova funcionais correlaçõe dentro da conexão adiabática.^[2]

• 5Leitura complementar

Definição e solução

O Hamiltoniano eletrônico em unidades atômicas, é

${\displaystyle {\hat {H}}=-{\frac {\nabla _{1}^{2}}{2}}-{\frac {\nabla _{2}^{2}}{2}}+{\frac {1}{u}}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle u}$ é a distância intereletrônica. Para os estados singletos, pode ser mostrado^[3] que a função de onda ${\displaystyle }$ satisfaz a equação de Schrödinger

${\displaystyle \left({\frac {u^{2}}{4R^{2}}}-1\right){\frac {d^{2}S(u)}{du^{2}}}+\left({\frac {3u}{4R^{2}}}-{\frac {1}{u}}\right){\frac {dS(u)}{du}}+{\frac {1}{u}}S(u)=ES(u)}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Introduzindo a variável adimensional ${\displaystyle x=u/2R}$, isso se torna uma função de Heun com pontos singulares em ${\displaystyle x=-1,0,+1}$. Com base nas conhecidas soluções de Heun, buscamos funções de onda da forma

${\displaystyle S(u)=\sum _{k=0}^{\infty }s_{k}\,u^{k}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e substituição na equação anterior produz arelação de recorrência

${\displaystyle s_{k+2}={\frac {s_{k+1}+\left[k(k+2){\frac {1}{4R^{2}}}-E\right]s_{k}}{(k+2)^{2}}}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

com os valores iniciais ${\displaystyle s_{0}=s_{1}=1}$. Assim, a condição de cúspide Kato é

${\displaystyle {\frac {S'(0)}{S(0)}}=1}$.

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A função de onda reduz para o polinomial

${\displaystyle S_{n,m}(u)=\sum _{k=0}^{n}s_{k}\,u^{k}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(onde ${\displaystyle m}$ o número de raízes entre ${\displaystyle 0}$ e ${\displaystyle 2R}$) se, e somente se, ${\displaystyle s_{n+1}=s_{n+2}=0}$. Assim, a energia ${\displaystyle E_{n,m}}$ é uma raiz da equação polinomial ${\displaystyle s_{n+1}=0}$ (onde ${\displaystyle \deg s_{n+1}=\lfloor (n+1)/2\rfloor }$) e o raio correspondente ${\displaystyle R_{n,m}}$ é encontrado a partir da equação anterior, o que gera

${\displaystyle R_{n,m}^{2}E_{n,m}={\frac {n}{2}}\left({\frac {n}{2}}+1\right)}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle S_{n,m}(u)}$ é a exata função de onda do ${\displaystyle m}$-esimo estado excitado da simetria singleto S para o raio ${\displaystyle R_{n,m}}$./////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Sabemos que a partir do trabalho de Loos e Gill que a energia HF do menor estado singleto S ${\displaystyle E_{\rm {HF}}=1/R}$. Segue-se que a exata correlação energia para ${\displaystyle R={\sqrt {3}}/2}$ é ${\displaystyle E_{\rm {corr}}=1-2/{\sqrt {3}}\approx -0.1547}$ que é muito maior do que a limitação da correlação das energias do íons como hélio (${\displaystyle -0.0467}$) ou os átomos de Hooke (${\displaystyle -0.0497}$). Isso confirma a visão de que a correlação de elétron na superfície de uma esfera é qualitativamente diferente do que em três dimensões de espaço físico.

Spherium em uma esfera tridimensional

Trabalhos recentes de Loos et al.^[4] considerado o caso de dois elétrons confinados em uma esfera tridimensional se repelindo coulombicalmente. Eles relatam um estado fundamental de energia de (${\displaystyle -.0476}$).

Química
História da química
Propriedades organolépticas
Cor | Brilho | Paladar | Odor
Propriedades físicas
Ponto de fusão | Ponto de ebulição | Tenacidade | Dureza | Densidade
Efeitos
Químico | Físico
Substâncias Puras
Elementos químicos
Misturas
Homogêneas | Heterogêneas
Efeitos Químicos
Combustão | Oxidação | Salificação | Corrosão | Fermentação | Hidrogenação | Hidrólise | Polimerização | Transesterificação | Fuligem | Fosforilação oxidativa | Aluminotermia | Esterificação
Combustão
Externa | Interna
Efeitos Físicos
Vaporização | Fusão | Solidificação | Condensação | Sublimação
Estados da matéria
Sólido | Líquido | Gasoso | Plasma | Condensado de Bose-Einstein
Tipos de vaporização
Ebulição | Calefação | Evaporação
Modos de separação de misturas
Catação | Ventilação | Levigação | Separação magnética | Peneiração | Flotação | Decantação | Centrifugação | Filtração | Destilação
Modos de destilação
Simples | Fracionada
Hidrocarbonetos
Alcanos Aromáticos | Alcadienos | Ciclanos | Ciclenos
Funções orgânicas
Álcoois | Haletos orgânicos | Fenóis | Enóis | Ácidos carboxílicos | Ésteres | Sais orgânicos
Ligações Químicas
Covalente | iônica | Metálica
Funções inorgânicas
Ácidos | Base | Sal | óxidos

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em química, a teoria dos orbitais moleculares é um método para determinar estruturas moleculares nas quais elétrons não são atribuídos a ligações químicas individuais entre átomos, ao invés disto são tratados como movimentos sob a influência do núcleo molecular.^[1]

Nesta teoria, cada molécula possui um conjunto de orbitais moleculares, nos quais se assume que a função de onda de cada orbital ψ_f pode ser descrita como uma combinação linear dos n orbitais atômicos χ_i, de acordo com a equação:^[2]

${\displaystyle \psi _{j}=\sum _{i=1}^{n}c_{ij}\chi _{i}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde c_ij podem ser determinados pela substituição destas equações pela equação de Schrödinger e pela aplicação do princípio variacional. Este método é conhecido como combinação linear de orbitais atômicos e é bastante utilizado pela química computacional. Uma transformação adicional unitária pode ser aplicada ao sistema para acelerar a convergência em alguns esquemas computacionais.

A teoria dos orbitais moleculares foi visto como um competidor à ligação de valência na década de 1930, hoje foi percebido que os dois métodos são relacionados e que quando generalizados eles se tornam equivalentes.

Em física computacional e química computacional, o método de Hartree–Fock (HF) é um método aproximativo para determinar a função de onda e a energia de um problema de muitos corpos de um estado estacionário.

O método de Hartree-Fock frequentemente considera que a função de onda de N corpos de um sistema pode ser aproximada por um único determinante de Slater (no caso de muitas partículas serem férmions) ou um permanent (no caso dos bósons) para N orbitais de spins. Utilizando o método variacional, pode-se derivar um conjunto de "N" equações acopladas para "N" orbitais de spins. Uma solução destas equações produz a função de onda de Hartree-Fock e dá a energia do sistema.

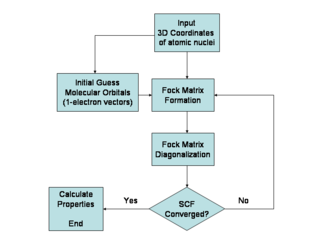
Na literatura o método de Hartree-Fock é chamado de método de campo autoconsistente. Ao deduzir o que hoje é chamada de equação de Hartree, como uma solução aproximada da equação de Schrödinger, Douglas Hartree exigiu que o campo final calculado a partir da distribuição de carga fosse autoconsistente com o campo considerado inicialmente. Assim, sua autoconsistência é uma exigência da solução. As soluções para as equações não lineares de Hartree-Fock também se comportam como se cada partícula fosse submetida ao campo médio criado por todas as outras partículas (operador de Hartree-Fock). As equações são universalmente resolvidas por meio de um método iterativo, embora o algoritmo de ponto fixo nem sempre convirja.^[1] Este tipo de solução não é a única possível e também não é uma característica essencial do método Hartree-Fock.

O método de Hartree-Fock encontra suas aplicações nas soluções da equação de Schrödinger para átomos, moléculas, nanoestruturas^[2] e em sólidos, mas também é usado em física nuclear. (Ver Hartree–Fock–Bogoliubov method para uma discussão da aplicação em física nuclear). Na teoria de estrutura atômica os cálculos devem ser feitos para um espectro de energia com muitos estados excitados. Desse modo o método de Hartree-Fock para átomos considera que a função de onda é uma única função de estado para a configuração atômica, com números quânticos bem definidos e que o nível de energia não é necessariamente o estado fundamental.

Para ambos átomos e moléculas, o método de Hartree-Fock é o ponto de partida para vários métodos de solução que descrevem precisamente o problema de muitos corpos.

O restante deste artigo se concentrará em aplicações da teoria da estrutura eletrônica adequada para moléculas, com o átomo como um caso especial. As discussões aqui são somente restritas ao método de Hartree-Fock, onde o átomo ou a molécula está em uma casca fechada com todos os orbitais (atômicos e molecular) duplamente ocupados. Os sistemas tipo casca aberta, onde alguns dos elétrons não estão emparelhados, podem ser tratados por um dos dois métodos de Hartree-Fock:

• Hartree-Fock de concha aberta restrita Restricted open-shell Hartree–Fock (ROHF)
• Hartree-Fock irrestrito Unrestricted Hartree–Fock (UHF)

• 9Ligações externas

Uma breve história

A origem do método de Hartree-Fock data do começo de 1920, logo após a descoberta da Equação de Schrödinger em 1926. Em 1927 Douglas Hartree introduziu o procedimento, que foi chamado de método do campo autoconsistente, para calcular aproximações para função de onda e energia para átomos e íons. Hartree foi guiado por alguns métodos anteriores, semi-empíricos, do início da década de 1920 (por E. Fues, R. B. Lindsay, e ele mesmo) de acordo com a Antiga teoria quântica de Niels Bohr.

No Modelo de Bohr do átomo, a energia do estado com número quântico n é dada em unidades atômicas ${\displaystyle E=-1/n^{2}}$. Observou-se então, a partir dos espectros atômicos, que os níveis de energia de átomos com muitos elétrons são bem descritos, aplicando uma versão modificada da fórmula de Bohr. Introduzindo o quantum defect d como parâmetro empírico, os níveis de energia de um átomo genérico são dados aproximadamente pela fórmula quantum defect, no sentido de que se pode reproduzir razoavelmente os níveis observados nas regiões de transição Raios X (veja a discussão empírica em Lei de Moseley). A existência de um quantum defect não zero foi atribuído à repulsão elétron elétron, que claramante não existe em um átomo de hidrogênio isolado. Essa repulsão é resultado screening effect da carga nuclear nua. Os primeiros pesquisadores mais tarde introduziram outros potenciais que continham parâmetros empíricos adicionais, com a esperança de reproduzir os dados experimentais.

Hartree procurou acabar com parâmetros empíricos e resolver a equação de Schrödinger independente do tempo de muitos-corpos a partir de princípios físicos fundamentais. Seu primeiro método de solução proposto ficou conhecido como Método de Hartree. Entretanto, muitos dos contemporâneos de Hartree não entenderam o raciocínio físico por trás do Método de Hartree. Para muitos sua conexão com a solução da equação de Schrödinger de muitos-corpos não estava clara. No entanto, em 1928 John C. Slater e J. A. Gaunt mostraram, independentemente, que o método de Hartree poderia ser formulado numa base teórica mais precisa, aplicando o princípio variacional a uma ansatz (função de onda de ensaio) como um produto de funções de partícula única.

Em 1930 Slater e Vladimir Fock, independentemente, apontaram que o método de Hartree não respeitava o princípio de função de onda para partículas idênticas. O método de Hartree usava o princípio de exclusão de Pauli em sua formulação mais velha, proibindo a presença de dois elétrons no mesmo estado quântico. No entanto, este método foi mostrado fundamentalmente incompleto, pois negligenciava a estatística quântica.

Foi então mostrado que um Determinante de Slater, um Determinante de orbitais de partícula única usados pela primeira vez por Heisenberg e Dirac em 1926, satisfez trivialmente as propriedades de Partículas idênticas da solução exata. E Portanto, era adequado usar um ansatz para aplicar o princípio variacional. O método de Hartree original pode então ser visto como uma aproximação ao método de Hartree-Fock negligenciando partículas idênticas. O método original de Fock se baseava fortemente na Teoria dos grupos, e era muito abstrato para os físicos contemporâneos entenderem e implementarem. Em 1935 Hartree reformulou o método para facilitar os cálculos.

O método de Hartree-Fock, apesar de fisicamente mais preciso, foi pouco usado até o advento dos computadores eletrônicos na década de 1950. Isso se deveu às demandas computacionais muito grandes do método Hartree e seus modelos empíricos. Inicialmente, tanto o método Hartree como o método Hartree-Fock foram aplicados exclusivamente a átomos, onde a simetria esférica do sistema permitiu simplificar bastante o problema. Esses métodos aproximados foram (e são) freqüentemente usados em conjunto com a aproximação de campo central, para que os elétrons na mesma casca tenham a mesma parte radial, e para restringir a solução variacional para serem autofunções do spin. Mesmo assim as soluções à mão para as equações de Hartree-Fock de um átomo de tamanho médio eram muito difíceis. E para pequenas moléculas elas requeriam recursos computacionais muito além do que estava disponível antes de 1950.

O algoritimo de Hartree-Fock

O método de Hartree-Fock é tipicamente usado para resolver a equação de Schrödinger independente do tempo para um átomo ou molécula de múltiplos elétrons como descrito na aproximação de Born-Oppenheimer. Como não há soluções conhecidas para sistemas de muitos elétrons (existem soluções para sistemas de um elétron como o átomo de hidrogênio), o problema é resolvido numericamente. Devido a não linearidade introduzida pela aproximação de Hartree-Fock, as equações são resolvidas usando um método não-linear como o de Iteração, que dá origem ao nome método do campo autoconsistente ^[3].

Aproximações

O método de Hartree-Fock faz cinco simplificações principais, são elas:

• A Aproximação de Born-Oppenheimer é utilizada. A função total da molécula é na verdade uma função das coordenadas de cada um dos núcleos, além da coordenada dos elétrons ^[3].
• Tipicamente os efeitos da relatividade especial são completamente negligenciados. O operador Momento é tido como não relativístico.
• A solução variacional é uma combinação linear de um número finito de funções de base, que normalmente são (mas nem sempre) escolhidas para serem ortogonais. O conjunto de base finita é assumido como sendo aproximadamente completo.
• Considera-se que cada auto-função da energia é descrita por um único determinante de Slater, um produto antisimétrico da funções de onda do elétron.
• A teoria do campo médio ou aproximação de campo médio, está implícita. Os efeitos decorrentes desses desvios, pressupõe que as correlações dos elétrons são completamente negligenciadas para os elétrons com spins opostos, mas são levados em conta para elétrons com spins paralelos. ^[4][5] (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.) ^[3][5]

Greatly simplified algorithmic flowchart illustrating the Hartree–Fock method

Otimização variacional dos orbitais

O método variacional mostra que para um operador Hamiltoniano independente do tempo, qualquer função de onda irá ter o valor esperado da energia, maior ou igual a energia do verdadeiro estado fundamental, dada pela função de onda do Hamiltonia fornecido. Devido a isso, a energia de Hartree-Fock é superior à verdadeira energia de estado fundamental de uma determinada molécula. No contexto do método de Hartree-Fock, a melhor possibilidade de solução é o Limite de Hartree-Fock, que é o limite em que a energia de Hartree-Fock se aproxima de uma base ortonormal (A outra é a configuração de iteração, onde as duas últimas aproximações do método de Hartree-Fock como descritas acima são desfeitas. Somente quando ambos os limites são alcançados que a solução exata, até a aproximação de Born-Oppenheimer, é obtida.). A energia de Hartree-Fock é a energia mínima de um único determinante de Slater.

O ponto de partida para o método de Hartree-Fock é um conjunto aproximado de funções de onda de um elétron conhecidas como spin-orbital. Para um cálculo orbital atômico, estes são tipicamente os orbitais de um átomo hidrogênio (um átomo com apenas um elétron, mas a carga nuclear apropriada). Para o cálculo do orbital molecular ou cristalino, as funções de onda de um elétron são tipicamente uma combinação linear de orbitais atômicos.

Os orbitais descritos acima apenas representam de maneira mediana a presença dos elétrons. No método de Hartree-Fock, o efeito dos muitos elétrons é contabilizado através da teoria de campo médio. Os orbitais são otimizados, exigindo que eles minimizem a energia do determinante de Slater. As condições variacionais resultantes nos orbitais levam a um novo operador de um elétron, chamado o operador Fock. Os orbitais ocupados são autosoluções do operador Fock, através de transformações unitárias entre si. O operador Fock é um eficiente operador Hamiltoniano de um elétron, sendo a soma de dois termos. O primeiro é uma soma de operadores da energia cinética para cada elétron, energia de repulsão internuclear, e da soma dos termos de atração eletrônica-nuclear Lei de Coulomb. O segundo são os termos Coulombianos de repulsão entre elétrons, descritos através da teoria de campo médio. É então calculada uma energia de repulsão líquida para cada elétron do sistema, tratando todos os elétrons dentro da molécula como uma distribuição suave de carga negativa. Essa é uma simplificação inerente ao método Hartree-Fock, e é equivalente à quinta simplificação da lista acima.

Desde que o operador Fock dependa dos orbitais usados para construir a matriz de Fock, as autofunções do operador Fock são, por sua vez, novos orbitais que podem ser usados para construir um novo operador Fock. Desta forma, os orbitais de Hartree-Fock são otimizados iterativamente até que a mudança na energia eletrônica total caia abaixo de um limiar predefinido. Dessa forma, um conjunto de orbitais autoconsistentes de um elétron são calculados. A função de onda eletrônica de Hartree-Fock é então dada pelo determinante de Slater construído fora destes orbitals. Seguindo os postulados da mecânica quântica, a função de onda de Hartree-Fock pode então ser usada para calcular qualquer propriedade química ou física desejada, dentro da estrutura do método de Hartree-Fock.

Formulação matemática

O operador de Fock

Como o termo de repulsão elétron elétron do Hamiltoniano molecular envolve as coordenadas de dois elétrons diferentes, é necessário reformulá-lo de forma aproximada. Para esta aproximação, todos os termos do Hamiltoniano exato, exceto o termo de repulsão nuclear, são reescritos como a soma dos operadores de um elétron para átomos ou moléculas em uma casca fechada (com dois elétrons em cada orbital).^[6] O "(1)" de cada símbolo de operador, indica que o operador é de um único elétron na natureza.

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)}$

É o operador de Fock para um elétron gerado pelos orbitais ${\displaystyle \phi _{j}}$,

${\displaystyle {\hat {H}}^{\text{core}}(1)=-{\frac {1}{2}}\nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha }}{r_{1\alpha }}}}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

É o núcleo do Hamiltoniano de um elétron,

${\displaystyle {\hat {J}}_{j}(1)}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde o operador de Coulomb define a energia de repulsão elétron elétron devido a cada um dos dois elétrons j no enésimo orbital.^[6]

${\displaystyle {\hat {K}}_{j}(1)}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

É o operador de troca, que define a energia de troca dos elétrons devido a antisimetrização da função de onda de todos os n elétrons.^[6] Onde o perador "Troca de energia", K, é obtido através do determinante de Slater. Então para encontrar as funções de onda de um elétron pelo método de Hartree-Fock, é equivalente a resolver as equações das autofunções:

${\displaystyle {\hat {F}}(1)\phi _{i}(1)=\epsilon _{i}\phi _{i}(1)}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde ${\displaystyle \phi _{i}\;(1)}$ são um conjunto de funções de onda um elétron, chamadas de orbitais moleculares de Hartree-Fock.

Na física atômica, o átomo de Bohr é um modelo que descreve o átomo como um núcleo pequeno e carregado positivamente cercado por elétrons em órbita circular.^[1]

Ernest Rutherford, no início do século XX, realiza o experimento conhecido como espalhamento de Rutherford ,^[2] no qual ele incidiu um feixe de partículas alfa (α) sobre uma folha de ouro e observou que, ao contrário do que era esperado - que as partículas deveriam ser refletidas pelos átomos de ouro considerados maciços até então -, muitas partículas atravessaram a folha de ouro e outras sofreram desvios. A partir da análise dessa experiência, afirmou que átomos eram constituídos de uma nuvem difusa de elétrons carregados negativamente que circundavam um núcleo atômico denso, pequeno e carregado positivamente.^[1]

A partir dessa descrição, é fácil deixar-se induzir por uma concepção de um modelo planetário para o átomo, com elétrons orbitando ao redor do "núcleo-sol". Porém, a aberração mais séria desse modelo é a perda de energia dos elétrons através da radiação síncrotron: uma partícula carregada eletricamente ao ser acelerada emite radiações eletromagnéticas que têm energia; fosse assim, ao orbitar em torno do núcleo atômico, o elétron deveria gradativamente emitir radiações e cada vez mais aproximar-se do núcleo, em uma órbita espiralada, até finalmente chocar-se contra ele. Um cálculo rápido mostra que isso deveria ocorrer quase que instantaneamente.

• 9Ligações externas

Postulado de Bohr

Através das descrições quânticas da radiação eletromagnética propostas por Albert Einstein e Max Planck, o físico dinamarquês Niels Bohr desenvolve seu modelo atômico a partir de quatro postulados:^[3]

1. Os elétrons que circundam o núcleo atômico existem em órbitas que têm níveis de energia quantizados.
2. A energia total do elétron (cinética e potencial) não pode apresentar um valor qualquer e sim, valores múltiplos de um quantum.^[1]
3. Quando ocorre o salto de um elétron entre órbitas, a diferença de energia é emitida (ou suprida) por um simples quantum de luz (também chamado de fóton), que tem energia exatamente igual à diferença de energia entre as órbitas em questão.
4. As órbitas permitidas dependem de valores quantizados (bem definidos) de momento angular orbital, L, de acordo com a equação

${\displaystyle \mathbf {L} =n\cdot \hbar =n\cdot {h \over 2\pi }}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde n = 1, 2, 3, ... é chamado de número quântico principal e h é a constante de Planck.^[4]

A regra 4 afirma que o menor valor possível de n é 1. Isto corresponde ao menor raio atômico possível, de 0,0529 nm, valor também conhecido como raio de Bohr. Nenhum elétron pode aproximar-se mais do núcleo do que essa distância.

O modelo de átomo de Bohr é às vezes chamado de modelo semi-clássico do átomo, porque agrega algumas condições de quantização primitiva a um tratamento de mecânica clássica. Este modelo certamente não é uma descrição mecânica quântica completa do átomo. A regra 2 diz que as leis da mecânica clássica não valem durante um salto quântico, mas não explica que leis devem substituir a mecânica clássica nesta circunstância. A regra 4 diz que o momento angular é quantizado, mas não diz por quê.

Expressão para o raio de Bohr

Considere o caso de um íon com a carga do núcleo sendo Ze e um eléctron movendo-se com velocidade constante v ao longo de um círculo de raio r com centro no núcleo.^[5]

A força de Coulomb sobre o electrão é

${\displaystyle F={\frac {Z.e^{2}}{4\pi \varepsilon _{o}r^{2}}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A força de Coulomb é a força centrípeta. Logo:

${\displaystyle F={\frac {Z.e^{2}}{4\pi \varepsilon _{o}r^{2}}}={\frac {m.v^{2}}{r}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Usando a regra de quantização do momento angular de Bohr:

${\displaystyle L=m.v.r={\frac {h}{2\pi }}=\hbar }$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Temos para o n-ésimo raio de Bohr:

${\displaystyle r_{n}={\frac {\varepsilon _{o}n^{2}h^{2}}{\pi .mZe^{2}}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

E a velocidade do electrão na n-ésima órbita:

${\displaystyle v_{n}={\frac {Z.{e}^{2}}{2\varepsilon _{o}h.n}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Equação de Rydberg

A equação de Rydberg, que era conhecida empiricamente antes da equação de Bohr, está agora na teoria de Bohr para descrever as energias de transições entre um nível de energia orbital e outro. A equação de Bohr dá o valor numérico da já conhecida e medida constante de Rydberg, e agora em termos de uma constante fundamental da natureza, inclui-se a carga do elétron e a constante de Planck.^[1] Quando o elétron é movido do seu nível de energia original para um superior e, em seguida, recua um nível retornando à posição original, resulta num fóton a ser emitido. Usando a fórmula derivada para os diferentes níveis de energia de hidrogênio, determinam-se os comprimentos de onda da luz que um átomo de hidrogênio pode emitir. A energia de um fóton emitido por um átomo de hidrogênio é determinado pela diferença de dois níveis de energia de hidrogênio:^[1]

${\displaystyle E=E_{f}-E_{i}=R_{E}\left({\frac {1}{n_{i}^{2}}}-{\frac {1}{n_{f}^{2}}}\right)\,}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde n_i é o nível inicial , e n_f é o nível final de energia. Uma vez que a energia de um fóton está

${\displaystyle E={\frac {hc}{\lambda }},\,}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

o comprimento de onda do fóton emitido é dada pela

${\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{n_{i}^{2}}}-{\frac {1}{n_{f}^{2}}}\right).\,}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Isto é conhecido como a equação de Rydberg, e o R da constante Rydberg é ${\displaystyle R_{E}/hc}$ , ou ${\displaystyle R_{E}/2\pi }$ em unidades naturais . Esta equação foi conhecida no século XIX pelos cientistas que estudavam a espectroscopia, mas não havia nenhuma explicação teórica para estas equações ou uma previsão teórica para o valor de R, até Bohr. A propósito, a derivação de Bohr da constante Rydberg, bem como o acordo concomitante da equação de Bohr com as experimentalmente observadas linhas espectrais de Lyman (${\displaystyle n_{f}=1}$), Balmer (${\displaystyle n_{f}=2}$), e Paschen (${\displaystyle n_{f}=3}$), e a previsão teórica bem sucedida de outras linhas ainda não observadas, foi uma das razões para o seu modelo ser imediatamente aceito. Para aplicar em átomos com mais de um elétron, a equação de Rydberg pode ser modificada pela substituição de "Z" por "Z - b" ou "n" por "n - b", em que b é uma constante que representa o efeito de triagem devido a outros elétrons. Isto foi estabelecido empiricamente antes de Bohr apresentar seu modelo.^[6]

Níveis energéticos dos elétrons em um átomo de hidrogênio

O modelo do átomo de Bohr explica bem o comportamento do átomo de hidrogênio e do átomo de hélio ionizado, mas é insuficiente para átomos com mais de um elétron.

Segue abaixo um desenvolvimento do modelo de Bohr que demonstra os níveis de energia no hidrogênio.

Sejam as seguintes convenções:

1. Todas as partículas são como ondas e, assim, o comprimento de onda do elétron, ${\displaystyle \lambda }$, está relacionado à sua velocidade por

${\displaystyle \lambda ={h \over m_{e}v}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde h é a constante de Planck e m_e, a massa do elétron. Bohr não tinha levantado esta hipótese porque só depois é que foi proposto o conceito associado a esta afirmação (veja dualidade onda-partícula). Porém, permite chegar na próxima afirmação.

2. A circunferência da órbita do elétron deve ser um múltiplo inteiro de seu comprimento de onda:

${\displaystyle 2\pi r=n\lambda \,}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde r é o raio da órbita do elétron e n, um número inteiro positivo.

3. O elétron mantém-se em órbita por forças eletrostáticas. Isto é, a força eletrostática é igual à força centrípeta:

${\displaystyle {kq_{e}^{2} \over r^{2}}={m_{e}v^{2} \over r}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle k={1 \over 4\pi \epsilon _{0}}}$ e q_e, a carga elétrica do elétron./////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Temos três equações e três incógnitas: v, ${\displaystyle \lambda }$ e r. Depois de manipulações algébricas para obter v em função das outras variáveis, pode-se substituir as soluções na equação da energia total do elétron:

${\displaystyle E=E_{cinetica}+E_{potencial}={1 \over 2}m_{e}v^{2}-{kq_{e}^{2} \over r}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Pelo teorema do virial, a energia total simplifica-se para

${\displaystyle E=-{1 \over 2}m_{e}v^{2}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E_{n}\,}$	${\displaystyle =-2\pi ^{2}k^{2}\left({\frac {m_{e}q_{e}^{4}}{h^{2}}}\right){\frac {1}{n^{2}}}\,}$
	${\displaystyle ={\frac {-m_{e}q_{e}^{4}}{8h^{2}\epsilon _{0}^{2}}}{\frac {1}{n^{2}}}\,}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ou, depois de substituídos os valores das constantes:^[7]

${\displaystyle E_{n}={\frac {-13.6\ \mathbf {eV} }{n^{2}}}\,}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Assim, o menor nível de energia do hidrogênio (n = 1) é cerca de -13.6 eV. O próximo nível de energia (n = 2) é -3.4 eV. O terceiro (n = 3), -1.51 eV, e assim por diante. Note que estas energias são menores que zero, o que significa que o elétron está em um estado de ligação com o próton presente no núcleo. Estados de energia positiva correspondem ao átomo ionizado, no qual o elétron não está mais ligado, mas em um estado desagregado.

O modelo atômico de Bohr pode ser facilmente usado para a composição do modelo atômico de Linus Pauling. Apenas somando as camadas e as colocando na ordem de Pauling.

Frequência

A frequência orbital^[5]

${\displaystyle f={\frac {\omega }{2\pi }}={\frac {v}{2\pi .r}}}$ (X)/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde ${\displaystyle \omega }$ é a velocidade angular orbital do elétron.

${\displaystyle {\frac {ke^{2}}{r^{2}}}={\frac {m.v^{2}}{r}}\Rightarrow \;m.v^{2}={\frac {ke^{2}}{r}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A partir da Equação - acima - do movimento orbital mantido pela força de Coulomb acima temos

${\displaystyle {\frac {v}{r}}={\sqrt {\frac {k.e^{2}}{m.r^{3}}}}}$/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Substituindo esta expressão na Equação (X) temos:

${\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k.e^{2}}{m.r^{3}}}}}$ (Z)/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Para o átomo - ${\displaystyle Hf=7x10^{15}Hz}$, /////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

a qual está na região ultravioleta do espectro electromagnético.

Se o elétron irradia, a energia E irá decrescer tornando-se cada vez negativa e a partir da Equação do raio da órbita r também diminui. O decréscimo em r na Equação (Z), provoca um aumento na frequência f.

De modo que temos um efeito de pista que quando a energia é irradiada, E diminui, o raio orbital r diminui, a qual por sua vez causa um aumento da frequência orbital f e aumentando continuamente a frequência irradiada.

Este modelo planetário prevê que o electrão se mova em espiral para dentro em direção ao núcleo, emitindo um espectro contínuo. Calcula-se que este processo não dure mais do que ${\displaystyle 1\times 10-8s}$, um tempo muito curto na verdade.