TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Tensor de Einstein

Origem: Wikipédia, a enciclopédia livre.

Em geometria diferencial, o tensor de Einstein (também tensor de traço revertido de Ricci), nomeado em relação a Albert Einstein, é usado para expressar a curvatura de uma variedade de Riemann. Em relatividade geral, o tensor de Einstein aparece nas equações de campo de Einstein para a gravitação descrevendo a curvatura do espaço-tempo.

Definição

O tensor de Einstein ${\displaystyle \mathbf {G} }$ é um tensor de ordem definido sobre variedades riemannianas. Ele é definido como

${\displaystyle \mathbf {G} =\mathbf {R} -{\frac {1}{2}}\mathbf {g} R,}$

/////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle \mathbf {R} }$ o tensor de Ricci, ${\displaystyle \mathbf {g} }$ o tensor métrico e ${\displaystyle R}$ o escalar de curvatura de Ricci. Em notação com índices, o tensor de Einstein tem a forma

${\displaystyle G_{\mu \nu }=R_{\mu \nu }-{1 \over 2}g_{\mu \nu }R.}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Propriedades

O tensor de Einstein é simétrico, visto que o tensor de Ricci e o tensor métrico são simétricos,

${\displaystyle G_{\mu \nu }=G_{\nu \mu }\,}$.

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O tensor de Einstein tem divergência nula, como pode-se demonstrar combinando as equações de campo de Einstein ao fato de que o tensor de energia-momento tem divergência nula

${\displaystyle G^{\mu \nu }{}_{;\nu }=0\,.}$.

A condutividade térmica (${\displaystyle \kappa }$) quantifica a habilidade dos materiais de conduzir energia térmica. Estruturas feitas com materiais de alta condutividade térmica conduzem energia térmica de forma mais rápida e eficiente do que estruturas análogas feitas com materiais de baixa condutividade térmica. Desta maneira, materiais com alta condutividade térmica são utilizados em dissipadores térmicos e materiais de baixa condutividade térmica são utilizados na confecção de objetos que visam a prover isolamentos térmicos, a exemplo, em cobertores. Esta propriedade, que é uma propriedade do material e não do objeto, guarda íntima relação com a equação de transporte de Boltzmann.

A condutividade térmica é uma característica específica de cada material e depende fortemente de sua pureza e da temperatura em que ele se encontrar (especialmente em baixas temperaturas). Em geral, a condução de energia térmica nos materiais aumenta à medida que a temperatura aumenta.^[1]

A condutividade térmica equivale numericamente à quantidade de calor ${\displaystyle Q}$ transmitida por unidade de tempo através de um objeto com espessura ${\displaystyle L}$ unitária, numa direção normal à área da superfície de sua seção reta ${\displaystyle A}$, também unitária, devido a uma variação de temperatura ${\displaystyle \Delta T}$ unitária entre as extremidades longitudinais. O inverso da condutividade térmica é a resistividade térmica.^[2]

A unidade de condutividade térmica segundo o sistema internacional de unidades é o watt por metro e por kelvin, sendo o watt obviamente análogo ao joule por segundo.

• 9Ligações externas

Definição matemática

Matematicamente, a condutividade térmica relaciona a quantidade de calor ${\displaystyle \Delta Q}$ transmitida por intervalo de tempo ${\displaystyle \Delta t}$ (a potência térmica) através de uma barra de material de comprimento ${\displaystyle L}$, na direção normal à seção reta de área ${\displaystyle A}$, com a diferença de temperaturas ${\displaystyle \Delta T}$ imposta às extremidades longitudinais. Assume-se o sistema em regime estacionário, e que não há fontes de calor laterais além da atrelada à manutenção da citada diferença de temperaturas entre as extremidades. ^[3] Matematicamente:

${\displaystyle {\frac {\Delta Q}{\Delta t}}.{\frac {L}{A}}=\kappa .\Delta T}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

De onde conclui-se que a condutividade térmica ${\displaystyle \kappa }$ do material do qual a barra é feito pode ser experimentalmente determinada pela relação:

${\displaystyle \kappa ={\frac {\Delta Q}{\Delta t}}.{\frac {L}{A\Delta T}}}$.

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

uma vez que todos os termos à direita são grandezas experimentalmente mensuráveis.

Unidades de medida e medição

No Sistema Internacional de Unidades (SI), a unidade de medida de condutividade térmica é o watt por metro-kelvin — simbologia: W/(m·K), W·m^-1·K^-1 ou W/m/K. A quantidade recíproca à condutividade térmica é a chamada resistividade térmica que, no Sistema Internacional de Unidades, tem por unidade o metro-kelvin por watt (m·K·W^-1 ou m·K/W).

Existem várias maneiras de se medir a condutividade térmica. A escolha do método a ser empregado depende do sistema em questão, da temperatura média do sistema, e varia também de acordo com as grandezas com as quais se quer estabelecer a dependência.

Há uma distinção entre técnicas de estado estacionário e técnicas de estado transiente. Em geral, as técnicas de estado estacionário são úteis quando a temperatura do material não muda com o tempo. Isso faz com que a análise do sinal seja direta, uma vez que estados estacionários implicam em sinais constantes. A desvantagem desses métodos é que uma boa engenharia experimental é necessária. Já as técnicas de transiente realizam medições durante o processo de aquecimento. Sua vantagem é a de ser um processo de medida mais rápido. Esses métodos normalmente são realizados por sondas do tipo agulha.

Fatores que influenciam a condutividade

Como dito anteriormente, podemos ver que seu valor depende diretamente do material em questão. A seguir, vamos citar outros fatores que influenciam o valor da condutividade térmica.

Fase do material

Quando um material sofre uma mudança de fase de sólido para líquido ou de líquido para gás, a condutividade térmica geralmente muda. Um exemplo é a mudança na condutividade térmica que ocorre quando a água em sua forma sólida, com condutividade térmica de 2,18 W*m^-1*K^-1 a 0 °C, derrete e passa a ter condutividade térmica de 0,58 W*m^-1*K^-1 a 0 °C quando em sua forma líquida. Isso se deve ao fato de que o calor se dá de maneira diferente para cada estado da matéria:

Gases: a transferência de calor por condução se dá através da colisão entre os átomos ou moléculas do gás e, por serem meios mais dispersos, a condutividade é pequena em comparação com a maioria dos sólidos.

Sólidos não metálicos: nestes a transferência de calor se dá através das vibrações da rede. Essa transferência é descrita através de fônons, os quanta das vibrações da rede.

Sólidos metálicos: esses são os melhores condutores de calor. Isso se dá porque os mesmos os elétrons livres responsáveis pela condução elétrica nos metais também participam de maneira significativa do processo de condução térmica. A condução por elétrons justapõe-se à transmissão via vibrações da rede, e a condução térmica dá-se de forma bem mais eficiente.

Estrutura do material

Um cristal puro apresenta condutividade térmica diferente ao longo de cada um dos seus diferentes eixos cristalinos, pois há diferenças no acoplamento dos fônons ao longo dos diferentes eixos do cristal.

Condutividade elétrica

Nos metais, a condutividade térmica esta relacionada com a condutividade elétrica de acordo com a lei Wiedemann-Franz, uma vez que os elétrons de condução, além de possibilitarem a corrente elétrica, transferem também energia térmica. No entanto, a correlação entre a condutância elétrica e a térmica só vale para metais, devido a forte influência dos elétrons no processo de transferência de eletricidade e dos fônons no processo de transferência de energia térmica.

Convecção

Revestimentos cerâmicos com baixa condutividade térmica são usados ​​em sistemas de escape para impedir que o calor atinja componentes sensíveis

O ar e outros gases, na ausência de convecção, geralmente são bons isolantes térmicos. Por isso, muitos dos materiais são isolantes por apresentarem poros que permitem o armazenamento de gases contudo impedem a convecção em grande escala. Exemplos destes materiais incluem polímeros porosos como o isopor, e o aerogel de sílica. Outros isolantes naturais são os biológicos, tais como pelos e penas, que protegem as peles dos animais contra agentes externos. As peles que possibilitam a produção de couro são também excelentes isolantes térmicos.

As cerâmicas são utilizadas nos sistemas de escape para evitar que haja calor sobre componentes a esse sensíveis. Gases pouco densos, como hidrogênio e hélio, normalmente têm condutividade térmica mais acentuada. Já gases densos como xenonio e diclorodifluorometano apresentam baixa condutividade térmica. Uma exceção é o hexafluoreto de enxofre, um gás denso com alta condutividade térmica, devido à sua capacidade térmica elevada. Argônio é um gás mais denso que o ar, e frequentemente é utilizado para preencher o interior de janelas com vidros duplos a fim de melhorar suas características de isolamento térmico.

Condutividade térmica de materiais a 27 °C (300 K)

Material	Condutividade térmica (Κ)
metais	[Κ] = W·m-1·K-1 (J·s-1·m-1·K-1)
Grafeno	4115[4] (Valor Médio)
Alumínio	237[5]
Cobre	401[5]
Ferro	80,2[5]
Ouro	317[5]
Prata	429[5]
Tungstênio	174[5]
outros materiais	[Κ] = W·m-1·K-1 (J·s-1·m-1·K-1)
Grafite pirolítico	195 (planar)[5]   5,70 (perpendicular)[5]
Vidro	0,79 (valor médio)
Tijolo	0,6 (valor médio)
Madeira (pinho)	0,13 (valor médio)
Fibra de vidro	0,05
Epoxi	0,30 (cargueada com sílica)   0,15 (não cargueada)[6][7]
Espuma de poliestireno	0,03
Polipropileno	0,25[8]
Espuma de poliuretano	0,02
Água	0,61
Ar	0,03

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A tabela acima é autoevidente, contudo algumas considerações adicionais devem ser feitas. A exemplo, é um engano a informação em senso comum de que o ouro (Κ = 317 W·m^-1·K^-1) é melhor condutor térmico do que os materiais citados. Na temperatura ambiente, o melhor condutor de calor ainda é o grafeno^[4].

Entretanto, como meio de estabelecer conexões entre partes metálicas de diferentes elementos, de forma a possibilitar calor de uma superfície à outra, o ouro leva muita vantagem sobre os demais materiais, pois sua oxidação ao ar livre é extremamente baixa; resultando numa elevada durabilidade e bom contato físico, elétrico e térmico. Entre os materiais citados, o alumínio seria o pior material para tais tipos de conexões térmicas ou elétricas, devido à sua facilidade de oxidação e à baixa condutividade térmica da superfície oxidada. Por motivos semelhantes, uma conexão via peças de cobre douradas, ao estilo das encontradas nas placas mãe de computadores, também leva vantagens sobre o alumínio e outros metais.

Uma conexão entre superfícies feita de cobre, soldada com prata, constitui uma das melhores combinações práticas para se viabilizar tanto a condução térmica bem como a condução de eletricidade entre dois ou mais pontos.

Outras definições relacionadas à condutividade térmica

O inverso da condutividade térmica é a resistividade térmica, geralmente medida em kelvin-metros por watt (K-m/W). Ao lidar com uma quantidade conhecida de material, um objeto em específico, grandezas físicas importantes são a sua condutância térmica e sua propriedade recíproca, à resistência térmica, as quais podem ser facilmente determinadas a partir da geometria do objeto e da condutividade ou resistividade térmicas do material. Embora muito usadas em conjunto, não se deve contudo confundi-las, pois tais grandezas definem-se por diferentes relações constitutivas. A seguir, apresentamos algumas relevantes.

Condutância

Geralmente, a condutividade térmica é a quantidade de calor que passa por unidade de tempo através de uma prato circular de área ${\displaystyle A}$ unitária (1 m²) e espessura ${\displaystyle L}$ também unitária (1 m) quando a diferença de temperatura entre suas faces é unitária (1 K). Para um prato com condutividade térmica ${\displaystyle \kappa }$, a condutância térmica é dada por

${\displaystyle \kappa A/L}$ e é medida em W*K^-1.

A condutividade e a condutância térmicas são quantidades que guardam entre si relações análogas as que guardam entre si as grandezas condutividade elétrica e condutância elétrica.

Coeficiente de calor e outras grandezas

Outra quantidade interessante relacionada à solução de problemas envolvendo condução térmica é o coeficiente de transferência de calor U, grandeza derivada da incorporação da espessura do material à sua característica de natureza intrínseca. Esta quantidade é normalmente utilizada quando tem-se um sistema composto pela justaposição de diversas camadas de diferentes materiais, cada qual com sua espessura própria, sendo definida de forma a permitir uma soma simples a fim de se obter um coeficiente global para o sistema. A última grandeza determina a quantidade de energia, sob a forma de calor, que passa por segundo através de cada metro quadrado de superfície, quando a diferença de temperatura entre as extremidades do sistema composto é de 1 K.

${\displaystyle {\frac {\Delta Q}{\Delta t}}=P=UA\Delta T}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde P é a potência térmica atrelada ao sistema.

A relação entre a condutividade térmica e o coeficiente de transferência de calor é dada por

${\displaystyle U={\frac {\kappa }{L}}}$.

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A reciproca do coeficiente de transferência de calor é o isolamento térmico. Em resumo:

Condutância térmica ${\displaystyle =\kappa A/L}$, cuja unidade é o watt por kelvin (W/K), propriedade do objeto.

Resistência térmica ${\displaystyle =L/(\kappa A)}$, cuja unidade é o kelvin por watt (K/W); propriedade do objeto.

Coeficiente de transferência de calor ${\displaystyle =\kappa /L}$, cuja unidade é o watt por kelvin e por metro quadrado (W/(K.m²)).

Isolação térmica ${\displaystyle =L/\kappa }$, medida em kelvin metro quadrado por watt (K.m²/W).

Resistência térmica

Conforme definida acima, a resistência térmica de um sistema (objeto) ou seção reta desse define-se como a razão entre o comprimento da seção e a condutividade térmica do material do qual é feita.

Quando temos resistências térmicas em série, estas são adicionadas. Assim, quando há calor através de duas seções justapostas, cada um com uma resistência de 1 °C*W^-1, a resistência total é de 2 °C*W^-1. Um dos problemas mais comuns no design de engenharia envolve a seleção de um dissipador térmico com tamanho adequado para uma determinada fonte de calor. Trabalhar em unidades de resistência térmica simplifica o projeto. A seguinte fórmula pode ser usada para estimar o desempenho

${\displaystyle R_{hs}={\frac {\Delta T}{P_{th}}}-R_{s}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle R_{hs}}$ é a resistência térmica máxima do dissipador de calor à temperatura ambiente, ${\displaystyle P_{th}}$ é a potência térmica e ${\displaystyle R_{s}}$ é a resistência térmica da fonte de calor.

Transmissão

Um terceiro termo é a transmitância térmica, que incorpora a condutividade térmica de uma estrutura com a transferência de calor devido à convecção e a radiação. Esta é medida nas mesmas unidades da condutividade térmica e é conhecida como a condutibilidade térmica de compósito.

Calor específico é uma grandeza física intensiva que define a variação térmica de determinada substância ao receber determinada quantidade de calor. Também é chamado de capacidade térmica mássica. A unidade no SI é J/(kg.K) (joule por quilograma e por kelvin). Uma unidade usual bastante utilizada para calores específicos é cal/(g °C) (caloria por grama e por grau Celsius).^[1]

Em rigor há dois calores específicos distintos: o calor específico a volume constante ${\displaystyle c_{v}}$ e o calor específico a pressão constante ${\displaystyle c_{p}}$. O calor específico a pressão constante é geralmente um pouco maior do que o calor específico a volume constante, sendo a afirmação verdadeira para materiais com coeficientes de dilatação volumétrico positivos. Em virtude do aumento de volume associado à dilatação térmica, parte da energia fornecida na forma de calor é usada para realizar trabalho contra o ambiente a pressão constante e não para aumentar a temperatura em si; o aumento de temperatura experimentado para um sistema à pressão constante é pois menor do que aquele que seria experimentado pelo mesmo sistema imposto o volume constante uma vez mantida a mesma transferência de energia na forma de calor. No caso do calor específico a volume constante, toda a energia recebida na forma de calor é utilizada para elevar a temperatura do sistema, o que faz com que ${\displaystyle c_{v}}$ — em virtude de sua definição — seja um pouco menor. A diferença entre os dois é particularmente importante em gases; em sólidos e líquidos sujeitos a pequenas variações de volume frente às variações de temperatura, os valores dos dois na maioria das vezes se confundem por aproximação. Em análise teórica e de precisão, contudo, é importante a diferenciação dos dois.

Materiais com dilatação anômala, como a água entre 0 °C e 4 °C, não obedecem à regra anterior; nestes casos o calor específico a volume constante é então um pouco maior do que o calor específico a pressão constante.

• • 6.1Bibliografia

Definição

O calor específico (${\displaystyle c\,\!}$) de uma substância pode ser definido a partir da capacidade térmica (${\displaystyle C\,\!}$) de um corpo composto por ela como o quociente desta pela massa (${\displaystyle m\,\!}$) desse corpo.^[2] Matematicamente,

${\displaystyle c={\frac {C}{m}}\,\!}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A capacidade térmica, por sua vez, é definida como a razão entre calor recebido e variação de temperatura observada. Assim, o calor específico pode ser expresso como:

${\displaystyle c={\frac {1}{m}}{\frac {\delta Q}{\delta T}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Por essa última relação, nota-se que o calor específico depende do processo pelo qual o calor é cedido à substância. Usando a primeira lei da termodinâmica, com ${\displaystyle p}$ sendo a pressão, pode-se escrever:

${\displaystyle c={\frac {1}{m}}{\frac {\mathrm {d} U+p\mathrm {d} V}{\mathrm {d} T}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Dois casos particulares são de maior importância. Um deles é o calor específico a volume constante, onde o termo representando o trabalho (${\displaystyle p\mathrm {d} V}$) é nulo, e pela relação anterior

${\displaystyle c_{v}={\frac {1}{m}}{\frac {\mathrm {d} U}{\mathrm {d} T}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O segundo caso é o calor específico a pressão constante. Nesse caso, a equação anterior resulta em

${\displaystyle c_{p}={\frac {1}{m}}{\frac {\mathrm {d} \left(U+pV\right)}{\mathrm {d} T}}}$,

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde a nova função de estado ${\displaystyle H=U+pV}$ é entalpia do sistema.^[3]

A distinção entre esses dois calores específicos pode normalmente ser ignorada nas fases sólida e líquida, dado que essas substâncias normalmente sofrem uma variação de volume muito pequena. Gases, no entanto, apresentam grande expansão térmica, sendo sempre necessária a distinção entre ambos os calores específicos.

Calor específico molar

Em muitas circunstâncias a unidade mais conveniente para especificar a quantidade de uma substancia é o mol, definido como sendo uma quantidade de 6,02 x 10²³ unidades elementares de qualquer substância. Assim, por exemplo um mol de alumínio significa 6,02 x 10²³ átomos de alumínio (o átomo é a unidade elementar), e 1 mol de óxido de alumínio significa 6,02 x 10²³ fórmulas moleculares do composto.

Nesses casos, quando a quantidade de substância é expressa em moles, utiliza-se o chamado calor específico molar, que é expresso como sendo a capacidade térmica por mol.^[4] De forma análoga com o calor específico por massa, o calor específico molar depende do processo ao qual a substância é submetida; define-se de mesma forma as quantidades a pressão constante e a volume constante.

Calor específico molar a volume constante

O calor específico molar a volume constante é definido como:

${\displaystyle c_{v}={\frac {Q}{n\Delta T}}={\frac {\Delta U}{n\Delta T}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Sendo que,

${\displaystyle \Delta U=Q-W}$ 

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(primeira lei da termodinâmica) com o trabalho ${\displaystyle W=0}$ temos ${\displaystyle \Delta U=Q}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

,por se tratar de um processo a volume constante.

onde:

• ${\displaystyle Q}$ é o calor absorvido ou cedido por uma amostra de ${\displaystyle n}$ moles de um gás;
• ${\displaystyle \Delta T}$ é a variação de temperatura resultante;
• ${\displaystyle \Delta U}$ é a variação de energia interna.

Para um gás monoatômico ideal,

${\displaystyle c_{v}={\frac {3}{2}}R=12,5J/mol/K}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Calor específico molar a pressão constante

O calor específico molar a pressão constante é definido como:

${\displaystyle c_{p}={\frac {Q}{n\Delta T}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Sendo que temos as seguintes relações:

${\displaystyle Q=U+W}$ (primeira lei da termodinâmica) e ${\displaystyle W=p\Delta V}$. Relacionando o trabalho com a equação dos gases ideais ${\displaystyle pV=nRT}$ ficamos com ${\displaystyle W=nR\Delta T}$. Substituindo a as respectivas equações mais a equação ${\displaystyle c_{v}={\frac {\Delta U}{n\Delta T}}}$ na equação ${\displaystyle Q=U+W}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 ficamos com

${\displaystyle c_{p}=c_{v}+R}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

• ${\displaystyle Q}$ é o calor absorvido ou cedido por uma amostra de ${\displaystyle n}$ mols de um gás;
• ${\displaystyle \Delta T}$ é a variação de temperatura resultante;
• ${\displaystyle \Delta U}$ é a variação de energia interna.

Regra de Dulong-Petit

A regra de Dulong-Petit consiste em obter, aproximadamente, o calor específico das substâncias por meio da massa molar:

${\displaystyle c\cong {\frac {3R}{M}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em que:

• ${\displaystyle c}$ é o calor específico, em joule por quilograma kelvin (J.kg⁻¹.K⁻¹);
• ${\displaystyle R}$ é a constante dos gases reais, equivalente a 8,31 joules por mol kelvin (J.K⁻¹.mol⁻¹);
• ${\displaystyle M}$ é a massa molar, em quilograma por mol (kg/mol).

Unidades

Sistema internacional

A unidade SI para calor específico é joule por kelvin por quilograma (J / K / kg, J / (kg K), JK ^-1 kg ^-1 , etc.). Como um incremento de temperatura de um grau Celsius é o mesmo que um incremento de um kelvin, é o mesmo que joule por grau Celsius por quilograma (J / ° C / kg). Às vezes, o grama é usado em vez de quilograma para a unidade de massa: 1 J / K / kg = 0,001 J / K / g.

O calor específico de uma substância (por unidade de massa) tem dimensão L ² · T − ² · Θ ⁻¹ ou (L / T) ² / Θ. Portanto, a unidade SI J / K / kg é equivalente ao metro quadrado por segundo ao quadrado por kelvin (m ² K ⁻¹ s ⁻² ).

Unidades de engenharia inglesas (imperiais)

Profissionais da construção , engenharia civil , engenharia química e outras disciplinas técnicas, especialmente no Estados Unidos , pode utilizar os chamados unidades de Inglês Engenharia , que incluem a imperial libra (lb = 0,45459237 kg) como unidade de massa, o grau Fahrenheit ou Rankine (° F = 5/9 K, cerca de 0,555556 K) como a unidade de incremento de temperatura, e a unidade térmica britânica (BTU ≈ 1055.06 J), ^[5] [6] como a unidade de calor.

Medição do calor específico de uma substância

Calorímetro

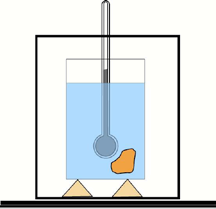
A capacidade calorífica de um corpo é determinada com ajuda de um calorímetro e um termômetro. Um calorímetro simples (veja a figura) consiste num cilindro metálico polido, colocado num outro cilindro metálico sobre cortiça (para isolamento térmico).^[7]

O calor específico de uma substância é normalmente determinado de acordo com a definição; ou seja, medindo a capacidade térmica de uma amostra da substância, geralmente com um calorímetro , e dividindo pela massa da amostra. Várias técnicas podem ser aplicadas para estimar a capacidade térmica de uma substância como, por exemplo, calorimetria de varredura diferencial rápida . ^[8] [9]

O cilindro interno é enchido com água ou algum outro líquido de calor específico conhecido. Um corpo de massa m, e capacidade calorífica específica c, aquecido a uma certa temperatura T é imergido no calorímetro de massa m₁ e capacidade calorífica c₁ na qual a temperatura é medida. Suponha que a temperatura deste líquido de m₂ e capacidade calorífica específica c₂ no calorímetro é T’ antes de o corpo ser emergido nele, e quando a temperatura do líquido e do corpo é a mesma, a temperatura torna-se T_f.

Da lei de conservação da energia e considerando o calor dissipado na vizinhança pelo objecto quente Q, o calor recebido pela água e pelo calorímetro que seja respectivamente Q₁ e Q₂ , mostra que a capacidade calorífica específica é

${\displaystyle c={\frac {c_{1}m_{1}(T_{f}-T)+c_{2}m_{2}(T_{f}-T')}{m(T-T_{f})}}={\frac {(c_{1}m_{1}+c_{2}m_{2})(T_{f}-T')}{m(T-T_{f})}}}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Fatores que afetam o calor específico

Representação de uma molécula vibrando.

Moléculas sofrem muitas vibrações características internas. A energia potencial armazenada nestes graus de liberdade internos contribui para uma amostra do conteúdo de energia, mas não a sua temperatura. Graus de liberdade mais internos tendem a aumentar a capacidade de uma substância de calor específico, contanto que as temperaturas são suficientemente elevadas para superar os efeitos quânticos.

Graus de liberdade

O comportamento termodinâmico das moléculas dos gases monoatômicos, como hélio, e dos gases diatômicos, como o nitrogênio, é muito diferente. Em gases monoatômicos, a energia interna é unicamente para movimentos de translação. Os movimentos são movimentos de translação em um espaço tridimensional em que as partículas se movem e trocam energia em colisões elásticas da mesma forma como fariam bolas de borracha colocadas num recipiente que foi agitado fortemente. (Veja animação aqui). Estes movimentos nas dimensões X, Y, e Z significam que os gases monoatômicos tem apenas três graus de liberdade de translação. Moléculas com maior atomicidade, no entanto, tem vários graus de liberdade interna, rotacionais e vibracionais. Elas se comportam como uma população de átomos que podem se mover dentro de uma molécula de formas diferentes (veja a animação à direita). A energia interna é armazenada nesses movimentos internos. Por exemplo, o nitrogênio, que é uma molécula diatômica, tem cinco graus de liberdade: três de translação e dois de rotação interna. Note que a calor específico molar a volume constante do gás monoatômico é ${\displaystyle {\frac {3}{2}}R}$, sendo R a constante universal do gás ideal, ao passo que para o valor do nitrogênio (diatômico) vale ${\displaystyle {\frac {5}{2}}}$, o que mostra claramente a relação entre os graus de liberdade e ao calor específico.

${\displaystyle c_{v}=({\frac {f}{2}})R}$ 

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle f}$ é o número de graus de liberdade.

Massa molar

Uma razão pela qual o calor específico tem valores diferentes para diferentes substâncias é a diferença de massas molares, que é a massa de um mol de qualquer elemento, que é diretamente proporcional à massa molecular do elemento, a soma dos valores das massas atômicas da molécula em questão. A energia térmica é armazenada pela existência de átomos ou moléculas de vibração. Se uma substância tem uma massa molar mais leve, em seguida, cada grama de que tem mais átomos ou moléculas disponíveis para armazenar energia. Esta é a razão pela qual o hidrogênio, a substância com menor massa molar tem um calor específico muito elevado. A consequência deste fenômeno é a de que, quando se mede o calor específico em termos molares a diferença entre substâncias torna-se menos acentuada e o calor específico de hidrogênio para de ser atípico. Da mesma forma, as substâncias moleculares (também absorvem calor em seus graus de liberdade internos) pode armazenar grandes quantidades de energia por mol se é moléculas grandes e complexas, e, portanto, seu calor específico medido em massa é menos perceptível . Uma vez que a densidade média de um elemento químico está fortemente relacionada com a sua massa molar, em termos gerais, há uma forte correlação inversa entre a densidade do sólido e o ${\displaystyle c_{p}}$ (calor específico a pressão constante). Lingotes sólidos grandes de baixa densidade tendem a absorver mais calor do que um lingote pequeno de mesma massa, porém com densidade mais elevada que o primeiro, porque contém mais átomos. Por conseguinte, em termos gerais, há uma forte correlação entre o volume de um elemento sólido e a sua capacidade total de calor. No entanto, existem muitos desvios desta correlação.

As ligações de hidrogênio

Contendo hidrogênio na sua composição, moléculas polares como o etanol, amônia e água, têm poderosas ligações intermoleculares de hidrogênio quando em sua fase líquida. Estas ligações proporcionam um outro local em que o calor pode ser armazenado como energia potencial de vibração, mesmo em baixas temperaturas comparativamente.

Impurezas

No caso de ligas, existem certas condições em que as pequenas impurezas podem alterar grandemente o calor específico medido. As ligas podem mostrar uma diferença marcada no seu comportamento, mesmo que a impureza em questão seja um dos elementos que formam a liga, tais como ligas impuras em semicondutores ferromagnéticos que podem conduzir a medições muito diferentes.

A tabela abaixo apresenta o calor específico de algumas substâncias à pressão constante de 1 atm.

Substância	Calor Específico (cal/g.°C)
água	1,0
álcool	0,58
alumínio	0,22
ar	0,24
carbono	0,12
chumbo	0,031
cobre	0,094
ferro	0,11
gelo	0,5
hélio	1,25
hidrogênio	3,4
latão	0,092
madeira	0,42
mercúrio	0,033
nitrogênio	0,25
ouro	0,032
oxigênio	0,22
prata	0,056
rochas	0,21
vidro	0,16
zinco	0,093

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ver também

O efeito fotoelétrico é a emissão de elétrons por um material, geralmente metálico, quando exposto a uma radiação eletromagnética (como a luz) de frequência suficientemente alta, que depende do material, como por exemplo a radiação ultravioleta. Ele pode ser observado quando a luz incide numa placa de metal, arrancando elétrons da placa. Os elétrons ejetados são denominados fotoelétrons.^[1]

Observado pela primeira vez por A. E. Becquerel em 1839 e confirmado por Heinrich Hertz em 1887,^[2] o fenômeno é também conhecido por "efeito Hertz",^[3][4] não sendo porém este termo de uso comum, mas descrito pela primeira vez por Albert Einstein, o efeito fotoelétrico explica como a luz de alta frequência libera elétrons de um material.^[5]

De acordo com a teoria eletromagnética clássica, o efeito fotoelétrico poderia ser atribuído à transferência de energia da luz para um elétron. Nessa perspectiva, uma alteração na intensidade da luz induziria mudanças na energia cinética dos elétrons emitidos do metal. Além disso, de acordo com essa teoria, seria esperado que uma luz suficientemente fraca mostrasse um intervalo de tempo entre o brilho inicial de sua luz e a emissão subsequente de um elétron. No entanto, os resultados experimentais não se correlacionaram com nenhuma das duas previsões feitas pela teoria clássica.

Em vez disso, os elétrons são desalojados apenas pelo impacto dos fótons quando esses fótons atingem ou excedem uma frequência limite (energia). Abaixo desse limite, nenhum elétron é emitido do material, independentemente da intensidade da luz ou do tempo de exposição à luz (raramente, um elétron irá escapar absorvendo dois ou mais quanta; no entanto, isso é extremamente raro porque ao absorver quanta suficiente para escapar, o elétron provavelmente terá emitido o resto dos quanta absorvidos). Para dar sentido ao fato de que a luz pode ejetar elétrons mesmo que sua intensidade seja baixa, Albert Einstein propôs que um feixe de luz não é uma onda que se propaga através do espaço, mas uma coleção de pacotes de ondas discretas (fótons), cada um com energia. Isso esclareceu a descoberta anterior de Max Planck da relação de Planck (E = hν), ligando energia (E) e frequência (ν) como decorrentes da quantização de energia. O fator h é conhecido como a constante de Planck.^[6][7][1] Em 1921 o alemão Albert Einstein recebeu o prêmio Nobel de Física por "suas contribuições para a física teórica e, especialmente, por sua descoberta da lei do efeito fotoelétrico."^[8]

• 5Referências

Descrição

Tomemos um exemplo: a luz vermelha de baixa frequência estimula os elétrons para fora de uma peça de metal; na visão clássica, a luz é uma onda contínua cuja energia está espalhada sobre a onda. Todavia, quando a luz fica mais intensa, mais elétrons são ejetados, contradizendo, assim a visão da física clássica que sugere que os mesmos deveriam se mover mais rápido (energia cinética) do que as ondas incidentes.

Quando a luz incidente é de cor azul, essa mudança resulta em elétrons muito mais rápidos. A razão é que a luz pode se comportar não apenas como ondas contínuas, mas também como feixes discretos de energia chamados de fótons. Um fóton azul, por exemplo, contém mais energia do que um fóton vermelho. Assim, o fóton azul age essencialmente como uma "bola de bilhar" com mais energia, desta forma transmitindo maior movimento a um elétron. Esta interpretação corpuscular da luz também explica por que a maior intensidade aumenta o número de elétrons ejetados - com mais fótons colidindo no metal, mais elétrons têm probabilidade de serem atingidos.

Aumentar a intensidade de radiação que provoca o efeito fotoelétrico não aumenta a velocidade dos fotoelétrons, mas aumenta o número de fotoelétrons. Para se aumentar a velocidade dos fotoelétrons, é necessário excitar a placa com radiações de frequências maiores e, portanto, energias mais elevadas.^[1]

Equações

Analisando o efeito fotoelétrico quantitativamente usando o método de Einstein, as seguintes equações equivalentes são usadas:

Energia do fóton = Energia necessária para remover um elétron + Energia cinética do elétron emitido

Mais detalhes em: Energia do fóton

Algebricamente:

${\displaystyle hf=\phi +E_{c_{max}}\,}$

///

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde:

• h é a constante de Planck,
• f é a frequência do foton incidente,
• ${\displaystyle \phi =hf_{0}\ }$ 
  ///

  TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  é a função trabalho, ou energia mínima exigida para remover um elétron de sua ligação atômica,
• ${\displaystyle E_{c_{max}}={\frac {1}{2}}mv_{m}^{2}}$ 
  ///

  TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  é a energia cinética máxima dos elétrons expelidos,
• f₀ é a frequência mínima para o efeito fotoelétrico ocorrer,
• m é a massa de repouso do elétron expelido, e
• v_m é a velocidade dos elétrons expelidos.

Notas:

Se a energia do fóton (hf) não é maior que a função trabalho (${\displaystyle \phi }$), nenhum elétron será emitido. A função trabalho é ocasionalmente designada por ${\displaystyle W}$.

Em física do estado sólido costuma-se usar a energia de Fermi e não a energia de nível de vácuo como referencial nesta equação, o que faz com que a mesma adquira uma forma um pouco diferente.

Note-se ainda que ao aumentar a intensidade da radiação incidente não vai causar uma maior energia cinética dos elétrons (ou electrões) ejectados, mas sim um maior número de partículas deste tipo removidas por unidade de tempo.