TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

A Física de partículas é um ramo da Física que estuda os constituintes elementares da matéria e radiação, assim como a interação entre elas e suas aplicações.^[1] É também chamada de física de altas energias, porque muitas partículas elementares só podem ser criadas em altas energias. O elétron e o próton foram as únicas partículas aceleradas até os dias de hoje, outras nunca foram detectadas (como o gráviton) e as restantes foram detectadas através da radiação cósmica (como o méson pi e o méson mu).

• 8Ligações externas

Breve história

Modelo Padrão da física de partículas
Partículas elementares do Modelo Padrão
Tópicos[Expandir]
Constituintes[Expandir]
Limitações[Expandir]
Cientistas[Expandir]
v d e

Os gregos antigos formularam dois conceitos sobre física de partículas. O primeiro foi formulado por Tales de Mileto e diz respeito à eletricidade. O segundo foi formulado por Demócrito e diz que toda matéria pode ser dividida até chegar em um ponto que se encontraria a parte mais fundamental e indivisível da matéria a que Demócrito deu o nome de átomo. Ele dizia que o átomo não poderia ser criado ou destruído e que toda a matéria conhecida seria formada por diversas combinações de diferentes átomos. Suas ideias se aproximavam muito dos atuais conceitos de física atômica.

As ideias de Demócrito só voltaram a ser revistas no século XIX, por Dalton. As de Tales de Mileto foram revistas a partir do século XV.

Principais partículas e antipartículas conhecidas: elétron, pósitron, próton, antipróton, nêutron, antinêutron, neutrino, antineutrino, mésons, híperons e fótons.

Diagramas de Feynman

Ver artigo principal: Diagrama de Feynman

Os diagramas de Feynman são utilizados para análise de processos quânticos. Originalmente, Feynman os desenvolveu para descrever a eletrodinâmica quântica, mas esta ferramenta passou a ser utilizada também na cromodinâmica quântica. Com uma grande variedade de interações entre partículas e com o desenvolvimento de teorias que incorporavam mais partículas nessas interações, responsáveis por mediá-las, os diagramas de Feynman são uma maneira simples de representar processos envolvendo partículas elementares.

Esses diagramas são representações no espaço-tempo com a coordenada espacial x em função da coordenada temporal ct. Usualmente, a coordenada temporal ct é representada na vertical e a espacial na horizontal, mas isso pode variar acordo com as preferências. As partículas são representadas por linhas retas com setas , de forma que estarão apontadas no sentido positivo do tempo se forem partículas, e estarão apontadas no sentido negativo se forem antipartículas. As linhas não representam trajetórias das partículas, uma vez que o objetivo está em descrever as interações entre elas apenas. Partículas virtuais são representadas por linhas tracejadas e só possuirão uma direção se forem partículas carregadas.

Modelo de Thomson

Partículas subatômicas

Ver artigo principal: Partícula subatômica

A pesquisa moderna da física da partícula é focalizada nas partículas subatômicas, que têm dimensões menores que as dos átomos. Incluem constituintes atômicos tais como elétrons (no modelo padrão ele é um lépton, junto com o múon, o tau e os respectivos neutrinos), prótons, e nêutrons (os prótons e os nêutrons são partículas compostas, feita de quarks), partículas produzidas por processos radiativos e de espalhamento tais como fótons, neutrinos, e múons, bem como uma larga escala de partículas exóticas.

• Elétron: Partícula mais conhecida e mais estudada, pertence a categoria de Léptons. Massa de repouso: 9,1083 x 10⁻³¹ kg, carga elétrica: − 1,602 x 10⁻¹⁹ C, Spin: 1/2 ħ.
• Pósitron: Já era previsto por Paul Dirac e sua existência foi confirmada em 1930–1940 pelo físico americano Anderson. É a antipartícula do elétron, possui massa de repouso e spin iguais aos do elétron. Carga elétrica de mesmo módulo e sinal contrário.
• Próton: É um núcleon partícula que se localiza no núcleo. Também pode ser classificada como um Bárion (tipo de partícula formada por 3 Quarks ligados por Glúons) e possui massa 1836,12 vezes a massa do elétron. Mesmo spin e carga de sinal contrário.
• Antipróton: Descoberto em 1955. Já se suspeitava que existissem outras antipartículas desde a descoberta do pósitron. Possui mesma massa e spin que o próton, mas carga de sinal oposto (sinal negativo).
• Nêutron: Como o próton, é um núcleon e também é classificado como Bárion. Possui carga nula, massa 1836,65 vezes a massa do elétron e spin 1/2 ħ. Pode se desintegrar dando origem a um próton, um elétron e um neutrino apenas quando está livre (fora do núcleo).
• Antinêutron: Possui exatamente as mesmas características do nêutron, mas organização interna diferente. Um nêutron é composto de um quark up e dois quarks down. Logo, imagina-se que o antinêutron seja formado por um antiquark up e dois antiquarks down.
• Fótons: É a partícula de mediação da força eletromagnética, classificada como bóson, são chamados de quantum do campo eletromagnético. Possui massa e carga elétrica zero e spin 1 ħ.
• Grávitons: Teoricamente é a partícula mediadora da força gravitacional, também sendo classificada como um bóson. Analogamente ao fóton, o gráviton é o quantum do campo gravitacional. Não se tem muita informação experimental sobre ele. Só existe com velocidades próximas ou iguais a c (velocidade da luz no vácuo).
• Mésons: São uma classe de hádrons quer dizer, massa média. São partículas que possuem massa entre a do elétron e a do próton.
• Híperons: Partículas de massa maior que a do próton.
• Neutrinos: O neutrino surge da desintegração de um nêutron em próton e elétron. Possui massa menor que 0,000005 vezes a massa do elétron e até agora foram descobertos quatro tipos de neutrinos diferentes.
• Glúon: é um bóson vetorial de massa nula. Há oito tipos de glúon. São partículas que intermedeiam a interação forte (assim como o fóton intermedeia a interação eletromagnética).
• Tau: é uma partícula subatômica da família dos léptons, sendo que ele é muito parecido com o elétron, ele pode ser genericamente chamado de elétron super-pesado. Sua anti-partícula é o anti-tau. Como no caso do elétron e do múon, o tau tem um neutrino associado, este é o neutrino de tau, seu tempo de vida é de cerca 2,9 × 10^-13s.
• Múon: é uma partícula elementar semi-estável com carga elétrica negativa e spin de 1/2 (férmion). Em conjunto com o elétron, o tau e seus respectivos neutrinos, é classificado como fazendo parte da família dos léptons.

Interações fundamentais

Ver artigo principal: Interações fundamentais

Todos os fenômenos físicos que ocorrem na natureza podem ser descritos em termos de quatro interações fundamentais. Elas são fundamentais no sentido de que não podem ser reduzidas a interações mais básicas. Cada interação descreve como uma dada característica, como a massa de uma partícula, ou conjunto de partículas, afeta outras partículas com essa mesma característica.

Segundo o modelo padrão, cada uma dessas interações é mediada pela troca de bósons entre as partículas na qual elas atuam. Essas partículas que mediam as interações são virtuais e, por isso, não podem ser observadas diretamente. Isso justifica o porquê de os efeitos dessas interações não serem sentidas instantaneamente, já que a maior velocidade que elas podem se propagar é com a velocidade da luz. Para que uma partícula virtual possa ser emitida sem violar a conservação de energia, a mesma deve ser reabsorvida em um intervalo de tempo tão curto quanto o permitido pelo princípio da incerteza. Porém, esses bósons mediadores podem ser tornar reais caso seja fornecida energia equivalente à energia de repouso deles.^[2]

Consequentemente o alcance de uma dada interação está relacionado com a massa do bóson mediador. Assim, quanto maior a massa do bóson mediador, menor será o alcance da interação. Cada interação também apresenta um chamado tempo de interação, de forma que a troca de bósons virtuais é feita dentro desse tempo.

A intensidade de cada interação é definida pela sua constante de acoplamento, um parâmetro adimensional que serve para comparar as diferentes interações. No caso particular da interação eletromagnética, a constante de acoplamento é obtida a partir da expressão da energia potencial eletrostática entre duas cargas puntiformes divida pelor fator ħc.

${\displaystyle V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A constante de acoplamento da interação eletromagnética é também conhecida como a constante de estrutura fina ${\displaystyle \alpha \approx 1/137}$, já substituindo os valores das constantes. Na tabela a seguir são apresentadas  características específicas de cada interação:^[

Eletrodinâmica quântica (EDQ), ou QED, de Quantum electrodynamics, é uma teoria quântica de campos do eletromagnetismo. A EDQ descreve todos os fenômenos envolvendo partículas eletricamente carregadas interagindo por meio da força eletromagnética. Sua capacidade de predição de grandezas como o momento magnético anômalo do múon e o desvio de Lamb dos níveis de energia do hidrogênio a tornou uma teoria renomada.

• 4Referências

História

A eletrodinâmica foi a evolução natural das teorias da antigamente denominada segunda quantização, isto é, quantização dos campos, ao ramo da eletrodinâmica.

As teorias de campo são necessariamente relativísticas, já que admitindo-se que haja partículas mensageiras na troca de energia e momento mediados pelo campo, essas mesmas partículas, a exemplo do fóton (que historicamente precedeu a descoberta das teorias de quantização do campo) devem se deslocar a velocidades próximas ou igual à da luz no vácuo (c = 299 792 458 m/s).

A primeira formulação da eletrodinâmica quântica é atribuída a Paul Dirac, que nos anos 1920 foi capaz de calcular o coeficiente de emissão espontânea do átomo.^[1] Essa teoria se desenvolveu a partir dos trabalhos Sin-Itiro Tomonaga, Julian Schwinger e Richard Feynman. Pelos seus trabalhos, eles ganharam o prêmio Nobel de Física em 1965.

Desenvolvimento formal

A eletrodinâmica quântica é uma teoria abeliana de calibre, dotada de um grupo de calibre U(1).

O campo de calibre que media a interação entre campos de spin 1/2, é o campo eletromagnético, que se apresenta sob a forma de fótons.

A descrição da interação se dá através da lagrangiana para a interação entre elétrons e pósitrons, que é dada por:

${\displaystyle {\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle \ \psi }$ e sua adjunta de Dirac ${\displaystyle \psi ^{*}}$ são os campos representando partículas eletricamente carregadas, especificamente, os campos do elétron e pósitron representados como espinores de Dirac.

Diamagnetismo é o termo utilizado para designar o comportamento de materiais que são repelidos na presença de campos magnéticos, ao contrário dos materiais paramagnéticos e ferromagnéticos que são atraídos por campos magnéticos.

Uma levitação diamagnética.

O diamagnetismo é um efeito quântico que existe em todos os materiais, mas é tão fraco que normalmente não pode ser observado quando o material possui uma das outras duas propriedades: ferromagnetismo ou paramagnetismo.^[1] Ou seja, o diamagnetismo corresponde ao tipo mais fraco de resposta magnética de um sistema.^[2]

Nos materiais diamagnéticos, os dipolos elementares não são permanentes, sendo que esses materiais não são afetados com a mudança de temperatura e o valor da sua susceptibilidade magnética é tipicamente próximo de milionésimo (10⁻⁶) e sempre negativo, devido a Lei de Lenz que afirma que um circuito submetido a um campo magnético externo variável, cria um campo contrário opondo-se a variação deste campo externo.^[2] Devido ao valor da susceptibilidade magnética ser negativo, o material sofre uma repulsão, entretanto o efeito é muito fraco, isto é, somente é percebido em campos magnéticos intensos, algumas ordens de grandeza maior do que o campo magnético terrestre.

Todo material diamagnético submetido a um campo magnético externo apresenta um momento dipolar magnético líquido orientado no sentido oposto ao do campo magnético externo. Se o campo magnético externo é não-uniforme, o material diamagnético é repelido da região onde o campo magnético é mais intenso para a região onde o campo magnético é menos intenso.^[1]

• 7Ligações externas

História

Foi primeiramente observado por Sebald Justinus Brugmans em 1778, ao observar que o bismuto e o antimônio eram repelidos por campos magnéticos. O diamagnetismo foi nominado e estudado por Michael Faraday, em 1845 que, através de seus estudos, concluiu que o diamagnetismo era uma propriedade da matéria, e que todo material respondia de uma forma diamagnética ou de uma forma paramagnética a um campo magnético aplicado a ele.^[3]

Materiais

Materiais diamagnéticos como a água, ou materiais que tenham a água como base, tem uma permeabilidade magnética relativa menor ou igual a 1, consequentemente sua susceptibilidade magnética é menor ou igual a zero, já que a susceptibilidade é definida por χ_v = μ_v − 1. Isso indica que materiais diamagnéticos são repelidos por campos magnéticos. Contudo, como o diamagnetismo é uma propriedade fraca, seus efeitos não podem ser observados no dia a dia. Por exemplo, a susceptibilidade magnética de diamagnéticos como a água é da ordem de χ_v = −9,05×10⁻⁶. O material diamagnético mais forte é o bismuto, χ_v = −1,66×10⁻⁴, mesmo que o grafite pirolítico possa ter susceptibilidade de χ_v = −4,00×10⁻⁴ em um dos planos. Mesmo assim, estes valores são de ordem de magnitude muito inferior ao magnetismo que possuem os materiais paramagnéticos e ferromagnéticos.

Todos os condutores mostram um diamagnetismo mais efetivo quando interagem com um campo magnético que varia no tempo. A força de Lorentz que age nos elétrons faz com que eles se movimentem formando correntes parasitas, que por sua vez produzem um campo magnético induzido no sentido oposto ao campo aplicado.

Supercondutividade

Transição da condutividade normal (esquerda) para a supercondutividade (direita). Durante a transição, o condutor repele o campo magnético e age como um diamagnético perfeito.

Supercondutores são materiais que perdem a resistência à corrente elétrica quando estão abaixo de uma determinada temperatura. O supercondutor é um diamagnético perfeito (χ_v = −1). pois ele repele todos os campos magnéticos (exceto em superfícies muito finas) devido ao Efeito Meissner. Esse efeito, que talvez seja a característica mais famosa dos supercondutores, é a causa da levitação magnética de um ímã, por exemplo, quando é colocado sobre um pedaço de supercondutor. A explicação para o fenômeno está na repulsão total dos campos magnéticos externos pelos supercondutores, o que faz com que o campo magnético interno seja nulo, desde que o campo externo aplicado não seja muito intenso.^[4]

Principais materiais diamagnéticos^[5] (O valor da susceptibilidade χ_v é adimensional)

Material	χv [x 10−5]
Supercondutor	-105
Grafite Pirolítico	-40,9
Bismuto	-16,6
Mercúrio	-2,9
Prata	-2,6
Diamante	-2,1
Chumbo	-1,8
Grafite	-1,6
Cobre	-1,0
Água	-0,91

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Teoria

Em um material, normalmente os elétrons se dispõe em órbitas, sem nenhuma resistência entre elas agindo como um loop de corrente. Deste modo, poderia se dizer que em geral os efeitos do diamagnetismo seriam comuns, visto que qualquer campo magnético aplicado gerariam corrente nesses loops em oposição à carga, de um modo similar aos supercondutores, que essencialmente são diamagnéticos perfeitos. Entretanto, como os elétrons são mantidos presos às órbitas pela carga dos prótons e ainda mais pelo Princípio de Exclusão de Pauli, muitos materiais exibem o diamagnetismo mas respondem muito pouco aos campos magnéticos aplicados.

O Teorema de Bohr-Van Leewen^[6][7] prova que não pode haver paramagnetismo ou diamagnetismo em um sistema puramente clássico, Porém, a teoria clássica de Paul Langevin para o diamagnetismo nos dá a mesma previsão que a teoria quântica. A teoria clássica é dada abaixo:

Diamagnetismo de Langevin

A teoria do diamagnetismo de Langevin^[8] se aplica a materiais que contém átomos O número de revoluções por unidade de tempo é com "cascas fechadas" (ver dielétrico). Um campo magnético com intensidade B, aplicado a um elétron com carga e e massa m, dá início à precessão de Larmor com uma frequência ω = eB / 2m. O número de revoluções por unidade de tempo é ω / 2π. Então a corrente elétrica para um átomo com Z elétrons é (em unidades do SI):

${\displaystyle I=-{Ze^{2}B \over 4\pi m}}$.

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O momento magnético de um loop de corrente é igual a corrente vezes a área do loop. Suponha que o campo é alinhado com o eixo z, a área média do loop pode ser dada por π(ρ²) , onde (ρ²) é a raíz quadrada da distância dos elétrons perpendiculares ao eixo z. O momento magnético é, portante:

${\displaystyle \mu =-{Ze^{2}B \over 4m}(\rho ^{2})}$.

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Se a distribuição da carga é esfericamente simétrica, podemos supor que a distribuição das coordenadas x, y, z são independentes e igualmente distribuídas. Então ${\displaystyle \langle x^{2}\rangle =\langle y^{2}\rangle =\langle z^{2}\rangle ={1 \over 3}\langle r^{2}\rangle }$.

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 Onde. ${\displaystyle \langle r^{2}\rangle }$é a raiz quadrada da distância dos elétrons até o núcleo, portanto ${\displaystyle \langle \rho ^{2}\rangle =\langle x^{2}\rangle +\langle y^{2}\rangle ={2 \over 3}\langle r^{2}\rangle }$.

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 Se n é o número de átomos por unidade de volume, a susceptibilidade magnética do volume é, em unidades do SI:

${\displaystyle \mathrm {X} ={\mu _{0}n\mu \over B}=-{\mu _{0}e^{2}Zn \over 6m}\langle r^{2}\rangle }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ferromagnetismo é o mecanismo básico pelo qual certos materiais (como ferro) formam ímãs permanentes, ou são atraídos por ímãs. Na física, vários tipos diferentes de magnetismo são distinguidos. Ferromagnetismo (incluindo ferrimagnetismo) é o tipo mais forte e é responsável por fenômenos comuns do magnetismo encontradas na vida cotidiana. Outras substâncias respondem fracamente a campos magnéticos com dois outros tipos de magnetismo o paramagnetismo, e o diamagnetismo, mas as forças são tão fracas que elas só podem ser detectadas por instrumentos sensíveis em um laboratório. Um exemplo corriqueiro de ferromagnetismo é um ímã de geladeira usado para guardar notas em uma porta do refrigerador.

Um material ferromagnético tem um momento magnético espontâneo – um momento magnético mesmo em um campo magnético aplicado igual a zero. A existência de um momento espontâneo sugere que os spins dos elétrons e os seus momentos magnéticos estão arranjados de uma maneira regular. O ferromagnetismo é encontrado em ligas binárias e ternárias de ferro, níquel, cobalto com outros elementos,^[1] alguns compostos de metais de terras raras, e alguns minerais de ocorrência natural, tais como magnetita.

• 9Bibliografia

História e distinção do ferrimagnetismo

Historicamente, o termo ferromagnético foi usado para qualquer material que exibisse magnetização espontânea, i.e, um momento magnético na ausência de um campo magnético externo. Esta definição geral é ainda de uso comum. Mais recentemente, no entanto, diferentes classes de magnetização espontânea foram identificadas. Em particular, um material é ferromagnético somente se todos os seus íons magnéticos adicionarem uma contribuição positiva para a magnetização líquida. Se alguns dos íons magnéticos subtrair a magnetização líquida (se forem parcialmente antialinhados), então o material é ferrimagnético. Se os momentos dos íons alinhados e antialinhados forem iguais, de modo a ter magnetização líquida zero, apesar do ordenamento magnético, então o material é um antiferromagneto. Estes efeitos de alinhamento só ocorrem em temperaturas abaixo de uma determinada temperatura crítica, denominada temperatura Curie (para ferromagnetos e ferrimagnetos) ou a temperatura Néel (para antiferromagneto).

Ciclo de histerese

Quando um campo magnético externo é aplicado a um ferromagneto como o ferro, os dipolos atômicos irão alinhar-se com ele. Mesmo quando o campo é removido, parte do alinhamento vai ser mantido: o material tornou-se magnetizado. Uma vez magnetizado, o imã vai ficar magnetizado por tempo indeterminado. Para desmagnetizar exige-se aplicação de calor ou de um campo magnético na direção oposta. Este é o efeito que fornece o elemento de memória em uma unidade de disco rígido.

A relação entre a indução magnética H e a magnetização M não é linear em tais materiais. Se um ímã é desmagnetizado (H = M = 0) e a relação entre H e M é plotada para aumento dos níveis de intensidade de campo, M segue a curva de magnetização inicial. Esta curva aumenta rapidamente no início e depois se aproxima de uma assíntota chamada saturação magnética. Se o campo magnético é agora reduzido monotonicamente, M segue uma curva diferente. Em uma intensidade de campo igual a zero, a magnetização é compensada a partir da origem de um montante chamado de remanência. Se a relação entre H e M for traçado para todas as forças de campo magnético aplicado o resultado é um ciclo de histerese chamado de loop principal.

Um olhar mais atento em uma curva de magnetização geralmente revela uma série de pequenos saltos aleatórios na magnetização chamados saltos Barkhausen. Este efeito é devido a defeitos cristalográficos tais como deslocamentos.

Origem física

O fenômeno da histerese em materiais ferromagnéticos é o resultado de dois efeitos: a rotação do vetor magnetização e as mudanças no tamanho ou número de domínios magnéticos. Em geral, a magnetização varia (em direção, mas não magnitude) através de um ímã.

Ímãs maiores são divididos em regiões chamadas de domínios. Em cada domínio, a magnetização não varia, mas entre os domínios temos paredes de domínio relativamente finas em que a direção da magnetização gira na direção de um domínio para outro. Se o campo magnético muda, as paredes se movem, mudando assim o tamanho relativo dos domínios.

Aplicações

Há uma grande variedade de aplicações da histerese em ferromagnetos. Muitos destes fazem uso de sua capacidade de reter memória, por exemplo, cartões de fita magnética, discos rígidos, e de crédito. Nestas aplicações, ímãs de disco rígido como o ferro são desejáveis para a memória não ser facilmente apagada.

Método de medição dos campos

O método descrito pelo ciclo de histerese mede o campo de indução magnética ${\displaystyle \mathbf {B} }$ em função do campo magnético ${\displaystyle \mathbf {H} }$. Se considerarmos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de ${\displaystyle \mathbf {H} }$ a partir da Lei de Ampère:

${\displaystyle \oint _{C}\mathbf {H} \cdot d\mathbf {l} =N\ I}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e, como o anel tem simetria circular, a integral resulta:

${\displaystyle H\cdot 2\pi R=N\ I\Longrightarrow H={\frac {N\ I}{2\pi R}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Levando em conta a permeabilidade magnética relativa do material ${\displaystyle \mu _{r}}$, é possível calcular o campo de indução magnética:

${\displaystyle B=\mu _{0}\mu _{r}\ H=\mu \ H}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Este sistema é usado na prática para medir os dois campos ao variar a intensidade da corrente:

${\displaystyle H\cdot 2\pi R=N\ I}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Uma vez medidos ${\displaystyle \mathbf {H} }$ e ${\displaystyle \mathbf {B} }$ se pode encontrar o valor da magnetização ${\displaystyle \mathbf {M} }$:

${\displaystyle \mathbf {H} ={\frac {\mathbf {B} -\mu _{0}\mathbf {M} }{\mu _{0}}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Por meio desse procedimento é possível obter experimentalmente a curva de magnetização, ou a variação do campo magnético em função do vetor de indução magnética e, portanto, o ciclo de histerese.

Temperatura de Curie

Marie Curie foi a primeira a descobrir que existe uma temperatura crítica para cada material ferromagnético acima da qual o material se comporta como paramagnético. Quando a temperatura aumenta, o movimento térmico compete com a tendência ferromagnética para os dipolos se alinharem. Quando a temperatura sobe além de certo ponto, chamado de temperatura Curie, há uma transição de fase de segunda ordem e o sistema não pode mais manter uma magnetização espontânea, embora ainda responda paramagneticamente a um campo externo. Abaixo dessa temperatura, há uma quebra espontânea de simetria e forma-se domínios aleatórios (na ausência de um campo externo). A Susceptibilidade magnética segue a lei de Curie-Weiss:

${\displaystyle \chi _{m}={\frac {C\ \rho }{T-T_{c}}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde C é uma constante característica do material, ${\displaystyle \rho }$ sua densidade e ${\displaystyle T_{c}}$ a temperatura de Curie em kelvin.

Modelos teóricos

O ferromagnetismo representa um dos principais problemas em aberto da física do estado sólido. Existem dois modelos teóricos que o descrevam: o modelo de Ising e o modelo de Weiss, o qual será tratado a seguir, ambos sendo baseados na hamiltoniana de Werner Karl Heisenberg, mas que utilizam grandes aproximações.

Hamiltoniana de Heisenberg

A hamiltoniana para um par de elétrons pertencentes a átomos vizinhos é:

${\displaystyle H=H_{1}+H_{2}+V_{12}\ }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle H_{1}}$ e ${\displaystyle H_{2}}$ são as hamiltonianas apenas dos elétrons, e ${\displaystyle V_{12}}$ é a interação entre os dois.

Pelo princípio de exclusão de Pauli, a função de onda total deve ser antissimétrica. Assim, tem-se duas possibilidades:

${\displaystyle \varphi _{A}=\psi _{S}(\mathbf {r} _{1},\mathbf {r} _{2})\chi _{A}(\mathbf {\sigma } _{1},\mathbf {\sigma } _{2})}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou

${\displaystyle \varphi _{A}=\psi _{A}(\mathbf {r} _{1},\mathbf {r} _{2})\chi _{S}(\mathbf {\sigma } _{1},\mathbf {\sigma } _{2})}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde os subscritos “A” ou “S” indicam uma função antissimétrica/simétrica.

As funções de onda de spin para um par de elétrons são:

${\displaystyle \chi _{S}:\left\{{\begin{matrix}|++\rangle \qquad [\mathbf {s} _{z}=1]\\{\frac {1}{\sqrt {2}}}(|+-\rangle +|-+\rangle )\quad [\mathbf {s} _{z}=0]\\|--\rangle \qquad [\mathbf {s} _{z}=-1]\\\end{matrix}}\right.}$

${\displaystyle \chi _{A}:{\frac {1}{\sqrt {2}}}(|+-\rangle -|-+\rangle )\quad [\mathbf {s} _{z}=0]}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

As funções de onda “espaciais” são:

${\displaystyle \psi _{S}:{\frac {1}{\sqrt {2}}}(\psi _{1}(\mathbf {r} _{1})\psi _{2}(\mathbf {r} _{2})+\psi _{1}(\mathbf {r} _{2})\psi _{2}(\mathbf {r} _{1}))}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle \psi _{A}:{\frac {1}{\sqrt {2}}}(\psi _{1}(\mathbf {r} _{1})\psi _{2}(\mathbf {r} _{2})-\psi _{1}(\mathbf {r} _{2})\psi _{2}(\mathbf {r} _{1}))}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Efetuando um cálculo perturbativo sobre tais funções de onda obtêm-se:

${\displaystyle E=\left\{{\begin{matrix}E_{0}+J\quad \rightarrow \quad \varphi _{1}=\psi _{S}\chi _{A}\\E_{0}-J\quad \rightarrow \quad \varphi _{2}=\psi _{A}\chi _{S}\\\end{matrix}}\right.}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde J é conhecida como integral de troca, que está relacionada com a Interação de Troca, interação responsável pela tendência dos momentos magnéticos do material a permanecerem paralelos entre si. A hamiltoniana separa, então, os estados com spins diferentes, e por este motivo, Heisenberg encontrou um operador que distinguisse os estados com spin diferente e que então pudesse descrever a interação precedente. Tal operador é:

${\displaystyle \mathbf {s} _{1}\cdot \mathbf {s} _{2}=\left\{{\begin{matrix}-{\frac {3}{4}}\quad \rightarrow \varphi _{1}\\{\frac {1}{4}}\quad \rightarrow \varphi _{2}\\\end{matrix}}\right.}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo, a Hamiltoniana de Heisenberg é:

${\displaystyle H_{Heisenberg}=-2J\mathbf {s} _{1}\cdot \mathbf {s} _{2}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Modelo de Weiss

O modelo de Weiss propõe a generalização da hamiltoniana de Heisenberg para um sistema com mais elétrons, utilizando uma aproximação de campo médio: um elétron sofre uma interação devida à média do campo gerado pelos outros elétrons.

A Hamiltoniana do sistema torna-se então:

${\displaystyle H_{magn}=g_{0}\mu _{B}\mathbf {s} (\mathbf {r} )\cdot \mathbf {B} -\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {s} (\mathbf {r} )\mathbf {s} (\mathbf {r} ')=s(\mathbf {r} )\cdot \langle g_{0}\mu _{B}\mathbf {B} -\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {s} (\mathbf {r} ')\rangle =}$

${\displaystyle =s(\mathbf {r} )g_{0}\mu _{B}\left(\mathbf {B} -{\frac {1}{g_{0}\mu _{B}}}\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {\langle } s(\mathbf {r} ')\rangle \right)}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle g_{0},\mu _{B}}$ são, respectivamente o fator giromagnético e o magnéton de Bohr.

Substituindo o momento magnético:

${\displaystyle \mathbf {m} =-g_{0}\mu _{B}\mathbf {s} }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

E o vetor magnetização:

${\displaystyle \mathbf {M} ={\frac {N}{V}}\langle \mathbf {m} \rangle }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Tem-se:

${\displaystyle H_{magn}=-\mathbf {m} (\mathbf {r} )\left(\mathbf {B} +\sum _{\mathbf {r} '}{\frac {J(\mathbf {r} -\mathbf {r} ')}{(g_{0}\mu _{B})^{2}}}{\frac {V}{N}}\mathbf {M} \right)}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo:

${\displaystyle H_{magn}=-\mathbf {m} (\mathbf {r} )(\mathbf {B} +\lambda \mathbf {M} )}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Percebe-se uma analogia com o paramagnetismo de Langevin, no qual se faz o mesmo tipo de estudo, substituindo-se o campo magnético por um campo magnético eficaz, dado por:

${\displaystyle \mathbf {B} +\lambda \mathbf {M} }$.

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Existe, assim, uma temperatura crítica de Curie:

${\displaystyle T_{C}={\frac {J_{0}s(s+1)}{3k}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Abaixo da qual se manifestam os efeitos do ferromagnetismo. As quantidades “s” e “k” são os autovalores do spin e a constante de Boltzmann respectivamente, enquanto ${\displaystyle J_{0}}$ é dado por:

${\displaystyle \sum _{\mathbf {r} '}{\frac {J(\mathbf {r} -\mathbf {r} ')}{(g_{0}\mu _{B})^{2}}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Materiais ferromagnéticos

A seguir, temos uma tabela com alguns materiais ferromagnéticos e suas respectivas temperaturas de Curie.

Material	Temp. Curie (K)
Fe	1 043
Co	1 388
Ni	627
Gd	292
Dy	88
MnAs	318
MnBi	630
MnSb	587
CrO2	386
MnOFe2O3	573
FeOFe2O3	858
NiOFe23	858
CuOFe2O3	728
MgOFe23	713
EuO	69
Y3Fe5O12	560

Ferromagnetismo é uma propriedade não apenas da composição química de um material, mas de sua estrutura cristalina e organização microscópica. Existem ligas de metal ferromagnético cujos constituintes não são próprios ferromagnéticos, chamado ligas de Heusler, em homenagem a Fritz Heusler. Por outro lado existem ligas não-magnéticas, como os tipos de aço inoxidável, compostas quase exclusivamente de metais ferromagnéticos.

No caso dos aços inoxidáveis, por exemplo, os da série 300, austeníticos (TP 304 ou TP 316), que contêm cromo e níquel em

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 sua composição química, não são magnéticos em seu estado recozido (mole) e são levemente magnéticos no estado encruado (duro). Já os aços inoxidáveis da série 400, ferríticos (TP 439 ou TP 444), que contêm apenas cromo em sua composição química, estes sim são magnéticos. Ademais, os aços inoxidáveis austeníticos, conquanto sejam, a priori, não magnéticos, podem ainda se tornarem parcialmente magnéticos ao sofrerem esforço mecânico durante um processo de conformação que lhes acarrete uma transformação de fase. ^[2][3]

Também se pode fazer ligas metálicas amorfas (não cristalinas) ferromagnéticas por resfriamento muito rápido de uma liga líquida. Estes têm a vantagem de que suas propriedades são quase isotrópicas (não alinhadas ao longo de um eixo do cristal), o que resulta em baixa coercividade, perda de baixa histerese, permeabilidade alta e alta resistividade elétrica. Um material desse tipo é normalmente uma transição liga metal-metalóide, feita a partir de cerca de 80% de metal de transição (normalmente Fe, Co, ou Ni) e um componente de metalóide (B, C, Si, P, ou Al) que reduz o ponto de fusão.

Uma classe relativamente nova de materiais ferromagnéticos excepcionalmente fortes são os ímãs de terras raras. Eles contêm elementos lantanídeos, que são conhecidos por sua capacidade de transportar grandes momentos magnéticos no bem localizado oribital f.

Ver também

• Antiferromagnetismo

O paramagnetismo consiste na tendência que os dipolos magnéticos atômicos têm de se alinharem paralelamente com um campo magnético externo. Este efeito ocorre devido ao spin mecânico-quântico, assim como o momento angular orbital dos elétrons. Caso estes dipolos magnéticos estejam fortemente unidos então o fenômeno poderá ser o ferromagnetismo ou o ferrimagnetismo.

Este alinhamento dos dipolos magnéticos atômicos tende a se fortalecer e é descrito por uma permeabilidade magnética relativa maior do que a sua unidade (ou, equivalentemente, uma susceptibilidade magnética positiva e pequena).

O paramagnetismo requer que os átomos possuam, individualmente, dipolos magnéticos permanentes, mesmo sem um campo aplicado, o que geralmente implica um átomo desemparelhado com os orbitais atômicos ou moleculares.

No paramagnetismo puro, estes dipolos atômicos não interagem uns com os outros e são orientados aleatoriamente na ausência de um campo externo, tendo como resultado um momento líquido zero. No caso de existir uma interação, então podem espontaneamente se alinhar ou antialinhar-se, tendo como resultado o ferromagnetismo ou o antiferromagnetismo, respectivamente. O comportamento paramagnético pode também ser observado nos materiais ferromagnéticos que estão acima da temperatura de Curie, e nos antiferromagnéticos acima da temperatura de Néel.

Em átomos sem dipolo magnético, um momento magnético pode ser induzido em uma direção anti-pararela a um campo aplicado, este efeito é chamado de diamagnetismo. Os materiais paramagnéticos podem também exibir o diamagnetismo, mas tipicamente com valores fracos.

Os materiais paramagnéticos em campos magnéticos sofrem o mesmo tipo de atração e repulsão que os ímãs normais, mas quando o campo é removido o movimento Browniano rompe o alinhamento magnético. No geral os efeitos paramagnéticos são pequenos (susceptibilidade magnética na ordem entre 10-3 e 10-5).

• 6Ligações externas

Lei de Curie

Sob baixos campos magnéticos, os materiais paramagnéticos exibem a magnetização na mesma direção do campo externo, e de acordo com a lei de Curie:

${\displaystyle \mathbf {M_{R}} =C\cdot {\frac {\mathbf {B} }{T}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

M_R é a magnetização resultante;

B é a densidade do fluxo magnético do campo aplicado, medido em tesla;

T é a temperatura absoluta, medida em kelvin;

C é uma constante específica de cada material (sua Constante de Curie).

Esta lei indica que os materiais paramagnéticos tendem a se tornar cada vez mais magnéticos enquanto o campo magnético aumentar, e cada vez menos magnéticos ao aumentar a temperatura. A lei de Curie é incompleta, pois não prediz a saturação que ocorre quando a maioria dos dipolos magnéticos estão alinhados, pois a magnetização será a máxima possível, e não crescerá mais, independentemente de aumentar o campo magnético ou diminuir-se a temperatura.

Materiais paramagnéticos

• Sódio Na [11] (metal alcalino)
• Magnésio Mg [12] (metal alcalino-terroso)
• Cálcio Ca [20] (metal alcalino-terroso)
• Estrôncio Sr [38] (metal alcalino-terroso)
• Bário Ba [56] (metal alcalino-terroso)
• Alumínio Al [13] (metal terroso) É o material paramagnético preferido para aplicações em catapultas eletromagnéticas lunares, utilizando rególito como minério.
• Oxigênio O [8] (ametal calcogênio) Na forma líquida.
• Tecnécio Tc [43] (metal de transição externa) (elemento artificial)
• Platina Pt [78] (metal de transição externa) (metal nobre)
• Urânio U [92] (metal de transição interna) (actinídeo)
• Óxido Nítrico NO [15] (composto gasoso da categoria dos monóxidos)

• ///////////

  TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ilustrações de prova do paramagnetismo

Pequenos imãs na ausência de um campo magnético

Pequenos imãs sob um campo magnético fraco

Pequenos imãs sob um campo magnético forte

Ver também

O fenômeno da supercondutividade

Um ímã levitando sobre um material supercondutor refrigerado a nitrogênio líquido, cuja temperatura é de aproximadamente -196 °C ou 77 K.

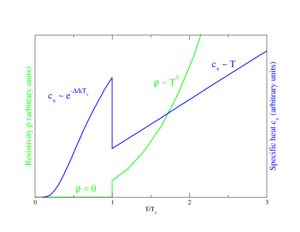
O que Kamerlingh Onnes observou foi que a resistência elétrica de alguns metais como o mercúrio, chumbo e estanho desapareciam completamente quando resfriados abaixo de uma temperatura crítica que é característica a cada tipo de material assim como a capacidade térmica.

O método mais simples de medir a resistência elétrica de algum material é colocá-lo em série num circuito elétrico com uma fonte de corrente determinada por I e medir a tensão elétrica V que atravessa o material. A resistência elétrica do material pode ser dada pela Lei de Ohm, na qual R=V/I. Se a tensão é igual a zero, isso significa que a resistência é também zero, e o material usado está no estado supercondutor.

Supercondutores são capazes de manter a corrente que os atravessa fluindo mesmo sem a aplicação de nenhuma tensão, propriedade essa explorada no estudo dos supercondutores eletromagnéticos como os encontrados nas máquinas MRI (imagem por ressonância magnética). Experimentos demonstraram que as correntes fluindo por anéis supercondutores podem persistir por anos sem decaimento algum. Evidências experimentais mostram que o tempo médio de existência da corrente chega a 100 mil anos. Já estimativas teóricas estimam que o tempo de duração destas correntes possa ser comparado ao tempo de existência do universo, dependendo da geometria e temperatura do fio supercondutor.

Num condutor normal, a corrente elétrica pode ser comparada a um fluido de elétrons se movendo por uma pesada rede iônica. Os elétrons estão em constante choque com os íons da rede, e durante cada colisão parte da energia carregada pelo elétron é absorvida pela rede e convertida em calor, que na verdade é chamada de energia cinética vibracional dos íons da rede. Assim a energia carregada pela corrente é constantemente dissipada, chamamos esse fenômeno de resistência elétrica.

Essa situação é diferente nos supercondutores. Num supercondutor convencional, o problema do fluido eletrônico não pode ser resolvido para elétrons individuais, mas sim para pares de elétrons, conhecidos como pares de Cooper. Esse pareamento é causado por uma força atrativa entre os elétrons pela troca de fônons. Assim como na Mecânica Quântica, o espectro de energia desse par de Cooper possui um gap de energia, que aqui significa o mínimo de energia ΔE que precisa ser aplicado para excitar esse fluido eletrônico. Esse valor de energia ΔE é maior que a energia térmica da rede dada por kT, em que k é a constante de Boltzmann e T é a temperatura, assim o fluido não é espalhado pela rede. Concluindo que o par de Cooper é um superfluido, significando que pode fluir sem dissipação de energia.

Existe ainda outra classe de supercondutores, conhecidos como supercondutores do tipo II, que incluem todos os supercondutores de altas-temperaturas. Uma pequena resistividade aparece em temperaturas não tão mais baixas do que a temperatura crítica para a transição supercondutora quando um campo elétrico é aplicado em conjunto com um campo magnético forte, que pode ser causado pela corrente elétrica. Isso pode ser comparado ao movimento de vórtices no superfluido eletrônico, que dissipa um pouco da energia carregada pela corrente elétrica. Se a corrente é relativamente pequena, esses vórtices se tornam estacionários, e a resistividade desaparece. A resistência provocada por esse efeito é pequena se comparada com a dos materiais não supercondutores, mas precisam ser levadas em conta nos experimentos. Entretanto, quando a temperatura cai suficientemente abaixo da temperatura de transição supercondutora, esses vórtices podem ficar parados dentro de uma fase desordenada, porém estacionária conhecida como vortex glass. Abaixo dessa temperatura de transição, a resistência desses materiais se torna realmente zero.

Transição de fase supercondutora

Comportamento da Capacidade Térmica (c_v, azul) e da Resistividade (ρ, verde) na transição de fase supercondutora

Nos materiais supercondutores, a característica da supercondutividade aparece quando a temperatura é abaixada até uma temperatura crítica (T_c). Esse valor de temperatura varia de material para material. Por convenção, supercondutores geralmente têm temperaturas críticas por volta de 20 K e até menores que 1 K. O mercúrio sólido, por exemplo, tem uma temperatura crítica de 4,2 K. Até 2009, a maior temperatura crítica encontrada para um supercondutor usual era de 39 K para o Diboreto de Magnésio (MgB₂).

Supercondutores de cupratos podem exibir temperaturas críticas muito maiores:

YBa₂Cu₃O₇, um dos primeiros cupratos supercondutores a ser descoberto, tem uma temperatura crítica da ordem de 92 K, e cupratos com base no mercúrio podem atingir temperaturas críticas próximas de 130 K. A explicação para o comportamento desses supercondutores para altas temperaturas ainda continua desconhecido. O pareamento entre elétrons e fônons explica a supercondutividade nos supercondutores convencionais, mas não explicam o comportamento dos supercondutores mais novos com temperaturas críticas mais altas.

Mesmo com a temperatura fixa abaixo da temperatura crítica, materiais supercondutores cessam sua supercondutividade quando um campo magnético externo, maior que o campo magnético crítico, é aplicado. Isso acontece porque a Energia Livre de Gibbs da fase supercondutora aumenta quadraticamente com o campo magnético enquanto a energia livre de uma fase normal é independente do campo magnético. Se o material é supercondutor na falta de um campo, então a fase supercondutora da energia livre é menor do que a energia na fase normal, e para valores finitos de campo magnético (proporcionais à raiz quadrada da diferença das energias livres num campo magnético nulo) as duas energias livres serão iguais a transição para fase normal ocorrerá. Generalizando, quanto maiores às temperaturas e os campos magnéticos, menor é a fração de elétrons na banda supercondutora e consequentemente leva a uma maior penetração de London de correntes e campos magnéticos externos. A profundidade de penetração tende ao infinito na transição de fase.

O início da supercondutividade num material é acompanhada por uma abrupta mudança em várias das propriedades físicas, que é o fator marcante na transição de fase. Por exemplo, a capacidade térmica eletrônica é proporcional à temperatura num regime normal, mas na transição supercondutora sofre um salto descontínuo e deixa de ser linear. A baixas temperaturas, esta variação é dada por e^-α/T, o comportamento exponencial é uma das evidencias da existência do gap de energia.

A ordem da transição da fase supercondutora foi uma questão amplamente debatida. Experimentos indicaram que a transição é de segunda ordem, isso significa que não há calor latente. No entanto na presença de um campo magnético externo há calor latente, isso acontece pelo fato de que na fase supercondutora a entropia é menor abaixo da temperatura crítica do que na fase normal. Como consequência disso, quando o campo magnético atinge valores maiores que o campo crítico, a transição de fase leva a uma diminuição na temperatura do material supercondutor.

O efeito Meissner

Ver artigo principal: Efeito Meissner

Efeito Meissner.

Walther Meissner e Robert Ochsenfeld concluíram que supercondutores quando colocados imersos em um campo magnético externo e resfriados abaixo da sua temperatura de transição, tendem a ejetar todo o campo magnético aplicado. Esse fenômeno é chamado de Efeito Meissner, mas não se resume apenas na ejeção do campo magnético por parte do supercondutor, pois na verdade o campo externo tende a penetrar o supercondutor mas apenas até uma certa profundidade definida por um parâmetro λ, denominado parâmetro de penetração de London, decaindo exponencialmente a zero na maior parte do material supercondutor. O efeito Meissner é uma característica primordial da supercondutividade, e para a maioria dos supercondutores λ é da ordem de 100 nm.

Muitas vezes o feito Meissner é erroneamente confundido com um tipo de diamagnetismo perfeito. Mas de acordo com a lei de Lenz quando promovemos uma mudança no campo magnético aplicado ao condutor e esse induz a criação de uma corrente elétrica que se opõe ao campo magnético. Em um condutor perfeito, uma corrente arbitrariamente grande pode ser induzida enquanto o campo resultante cancelaria o campo aplicado.

O efeito Meissner é de fato distinto, pois se observa a expulsão espontânea e abrupta do campo magnético interno que ocorre na transição supercondutora quando o material é resfriado abaixo da sua temperatura crítica, o que não seria de se esperar com base na lei de Lenz.

A explicação fenomenológica para o efeito Meissner foi dada pelos irmãos Heiz e Fritz London, que demonstraram que a energia eletromagnética livre em um supercondutor pode ser minimizada pela equação de London:

${\displaystyle \nabla ^{2}\mathbf {H} =\lambda ^{-2}\mathbf {H} \,}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde H é o campo magnético e λ é a profundidade de penetração de London.

Um supercondutor com pouco ou nenhum campo magnético em sue interior está no estado de Meissner, mas perde rapidamente esse estado quando o campo magnético externo aplicado é muito grande. Nos supercondutores do tipo I, a supercondutividade é abruptamente destruída quando a força do campo magnético ultrapassa um valor crítico H_c. Nos supercondutores do tipo II, quando o campo externo é aumentado até um valor crítico H_c1 leva a um estado intermediário (estado de vórtice), em que uma quantidade crescente de fluxo magnético penetra no material, mas sem apresentar resistência ao fluxo de corrente elétrica atingindo um valor crítico H_c2 onde a supercondutividade é destruída. O estado intermediário é causado pela passagem de vórtices no superfluido eletrônico, e às vezes são chamados de flúxions, pois o transporte por esses vórtices é quantizado.

O Gap de energia e a teoria BCS

Vídeo demonstrando a levitação por supercondutividade.

Um grande passo na evolução dos conhecimentos sobre os supercondutores é o estabelecimento da existência de um gap de energia Δ, da ordem de kT_c, entre o estado fundamental e as excitações das quasi-partículas do sistema. Esse conceito já havia sido sugerido por Daunt e Mendelssohn na tentativa de explicar a ausência de efeitos termoelétricos. Mas as primeiras evidências quantitativas e experimentais vieram com as medidas precisas do calor específico dos supercondutores feitas por Corak. Estas médias mostraram que o calor específico eletrônico é definido por uma dependência exponencial com:

${\displaystyle C_{es}=\gamma T_{c}ae^{-{\frac {bT_{c}}{T}}}}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde o estado normal do calor específico eletrônico é dado por C_en≈γT_c, e a e b são constantes numéricas.

A Teoria BCS foi proposta por John Bardeen, Leon Cooper, e John Robert Schrieffer e explica o fenômeno da supercondutividade.

A Teoria afirma principalmente que os elétrons em um material quando no estado supercondutor se agrupam em pares chamados pares de Cooper. Os pares de Cooper são elétrons condensados em estados de menor energia. Esta formação de pares de Cooper depende da microestrutura do material e da forma da rede cristalina, já que este par de elétrons se move de forma acoplada com a rede.

Independentemente e ao mesmo tempo, este fenômeno de supercondutividade foi explicado por Nikolay Bogoliubov por meio das então chamadas transformações de Bogoliubov.

Em muitos supercondutores, a interação atrativa entre elétrons (necessariamente aos pares) é conduzida aproximada e indiretamente pela interação entre os elétrons e a estrutura do cristal em vibração (os fônons).

Um elétron que se move através de um condutor atrairá cargas positivas próximas na estrutura. Esta deformação da estrutura faz com que outro elétron, com “spin” oposto, mova-se na região de uma densidade de carga positiva mais elevada. Os dois elétrons são mantidos unidos então com alguma energia de ligação. Se esta energia de ligação é mais elevada do que a energia fornecida por impulsos dos átomos de oscilação no condutor, então os pares de elétrons conseguem se manter juntos e resistem aos impulsos, não experimentando resistência.

A teoria BCS foi desenvolvida em 1957 e recebeu o Prêmio Nobel de Física em 1972.

Partindo da suposição que existe alguma atração entre elétrons, a qual pode suplantar a repulsão de Coulomb. Na maioria dos materiais (em supercondutores a baixa temperatura), esta atração é conduzida aproximadamente de maneira indireta pelo acoplamento dos elétrons à estrutura cristalina. As extensões da teoria de BCS existem para descrever outros casos, embora sejam insuficientes para descrever completamente as características observadas da supercondutividade de alta temperatura, mas é hábil para dar uma aproximação para o estado mecânico quântico do sistema de elétrons (atrativamente interagindo) dentro do metal. Este estado é sabido agora como de "o estado BCS". No estado normal de um metal, os elétrons movem-se independente, visto que no estado BCS, são ligados em pares de Cooper pelas interações atrativas.

Desde que os elétrons sejam limitados em pares de Cooper, uma quantidade finita de energia é necessária para separar estes dois elétrons independentes. Isto significa que há um gap de energia para a "excitação de partícula única", ao contrário dos metais normais (onde o estado de um elétron pode ser mudado adicionando arbitrariamente uma pequena quantidade de energia). Esta abertura de energia é mais alta a baixa temperatura, mas desaparece na temperatura de transição quando supercondutividade cessa de existir.

A teoria BCS corretamente prediz que a variação do gap com a temperatura. Igualmente dá uma expressão que mostra como este gap cresce com a força da interação atrativa e a (fase normal) da partícula única na densidade dos estados na energia de Fermi. Além disso, descreve como a densidade dos estados é mudada ao incorporar o estado supercondutor, onde não há qualquer estado eletrônico na energia de Fermi. O gap de energia é observada o mais diretamente em experiências de tunelamento e na reflexão das micro-ondas de supercondutor.

A teoria de Ginzburg-Landau

Embora boa parte deste trabalho siga a formato da teoria BCS, substancialmente predizendo vários processos como a relaxação nuclear e a atenuação ultrassônica em que o gap de energia e o espectro de excitação têm um papel essencial. A teoria de Ginzburg-Landau se concentra inteiramente no comportamento supercondutivo dos elétrons ao invés das excitações, e foi proposta em 1950, 7 anos antes da teoria BCS. Ginzburg e Landau introduziram uma pseudo-função de onda ψ complexa como um parâmetro dentro da teoria geral de Landau das transições de fase de segunda ordem. Esse ψ descreve os elétrons supercondutores, e a densidade local de elétrons supercondutores (definida pelas equações de London)

${\displaystyle \mathbf {n_{s}=|\psi (x)|^{2}} }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Então, usando um princípio variacional e trabalhando para assumir uma expansão em séries da energia livre em função de ψ e de ψ com a expansão dos coeficientes α e β, eles derivaram a seguinte equação diferencial para ψ:

${\displaystyle {\frac {1}{2m^{*}}}({\frac {\hbar }{i}}\nabla -{\frac {e^{*}}{c}}A)^{2}(\psi +\beta |\psi |^{2}\psi )=-\alpha (T)\psi }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

a equação acima é análoga a equação de Schrödinger para uma partícula livre, mas com um termo não linear. E a equação correspondente para a super-corrente elétrica fica:

${\displaystyle J_{s}={\frac {e^{*}\hbar }{i2m^{*}}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})-{\frac {e^{*}}{2m^{*}c}}|\psi |^{*}A}$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

que é na verdade uma expressão da corrente a partir mecânica quântica para partículas de carga e* e massa m*. Com esse formalismo os cientistas foram capazes de tratar dois problemas, com ajuda da [teoria de London]:

• Efeitos não lineares dos campos fortes o suficiente para mudar ns ou |ψ|²
• A variação espacial de n_s.

A grande contribuição desta teoria foi tratar do estado intermediário de alguns supercondutores, onde o estado normal e o supercondutor coexistem na presença de um campo magnético H~H_c.

Quando foi proposta, a teoria pareceu mais fenomenológica, e não foi dada a devida importância, especialmente na literatura ocidental. Mas de qualquer forma em 1959, Gor'kov foi capaz de mostrar que a teoria de Ginzburg-Landau era, de fato, uma forma da teoria BCS microscópica.

Supercondutores do Tipo II

Em 1957, o cientista russo Alexei Abrikosov publicou um artigo significativo onde investigava o que aconteceria caso a razão κ= λ/ξ da teoria de Ginzburg-Landau fosse grande ao invés de pequeno, se ξ<λ e não o contrário, o que levaria a uma energia de superfície negativa. Abrikosov concluiu que existiam dois tipos distintos de comportamento e chamou de supercondutores do tipo II os que apresentavam tal característica. Ele mostrou que o ponto exato de separação entre os dois regimes era quando κ=1/2. E para materiais com κ>1/2 ele descobriu que ao invés do desaparecimento descontinuo da supercondutividade na transição de primeira ordem em Hc, havia uma penetração contínua no fluxo começando com um campo crítico pequeno H_c1 alcançando B=H num campo crítico H_c2. Essa propriedade foi responsável por permitir magnetos supercondutores de altos campos.

Outro resultado importante na análise de Abrikosov foi que em um estado misto, também chamado de fase de Schubnikov, entre os valores críticos de H_c1 e H_c2 o fluxo pode não penetrar nos domínios laminares, mas num arranjo de fluxo tubular, cada um carrega um fluxo quântico.

${\displaystyle \mathbf {\phi _{0}=hc^{2}e=2,07x10^{-7}G-cm^{2}} }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em cada célula unitária do arranjo com formato triangular (menor energia livre) existe um vórtex de supercorrente concentrando o fluxo até o centro do vórtex. Concluindo então que os supercondutores do tipo II não são diamagnéticos perfeitos, e desde que |ψ|² seja zero no centro dos vórtices, não teremos gaps de energia nos núcleos. Levando a conclusão de que não podemos classificar os supercondutores como condutores perfeitos.

O Tunelamento de Josephson

Junção de Josephson, em arranjo feito pelo NIST para medida de tensão no SI

Agora sabendo que os supercondutores não poderiam mais ser entendidos como condutores perfeitos, a pergunta a ser feita era qual a característica universal que possuía o estado supercondutor. A resposta é a existência de funções de onda ψ(r) para muitos corpos, onde a amplitude a fase são quem mantém a coerência sobre as distâncias macroscópicas. Esse condensado é análogo, porém não idêntico, ao condensado de Bose-Einstein, com os pares eletrônicos de Cooper substituindo os bósons condensados no superfluido de hélio.

Desde que a fase e o número de partículas são variáveis conjugadas, refletindo os aspectos complementares do dualismo partícula-onda, a relação de incerteza é dada por:

${\displaystyle \Delta N\Delta \Phi \leq 1}$

onde o limite da precisão entre N e φ podem ser simultaneamente conhecidos.

O significado físico dos graus de liberdade da fase foram primeiramente enfatizados no trabalho de Josephson, que previu que os pares deveriam ser capazes de tunelar dois supercondutores a tensão zero, dando uma supercorrente de densidade:

${\displaystyle \mathbf {J=J_{c}sin(\Phi _{1}-\Phi _{2})} }$

///////////

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde J_c é uma constante e φ é a fase de ψ no iésimo supercondutor na junção do túnel. Josephson previu que a diferença de tensão entre os eletrodos deveriam causar a diferença de fase aumentar no tempo como 2eV12t/ℏ, assim a corrente poderia oscilar com uma frequência ω=2eV12/ℏ. As junções de Josephson foram utilizadas em voltímetros ultrassensíveis e magnetómetros, e também nas medidas mais acuradas da razão das constantes fundamentais ℏ/e. De fato, a medida padrão do volt é hoje definida em termos da frequência da corrente alternada de Josephson.